n = int(input())
price = list(map(int,input().split()))
dp = [[0]*(n+1) for _ in range(n+1)]
for i in range(1,n+1):
dp[i][1] = price[0]*i
for i in range(2,n+1):
for j in range(2,i+1):
dp[i][j] = max(price[j-1]+dp[i-j][i-j],dp[i][j-1] )
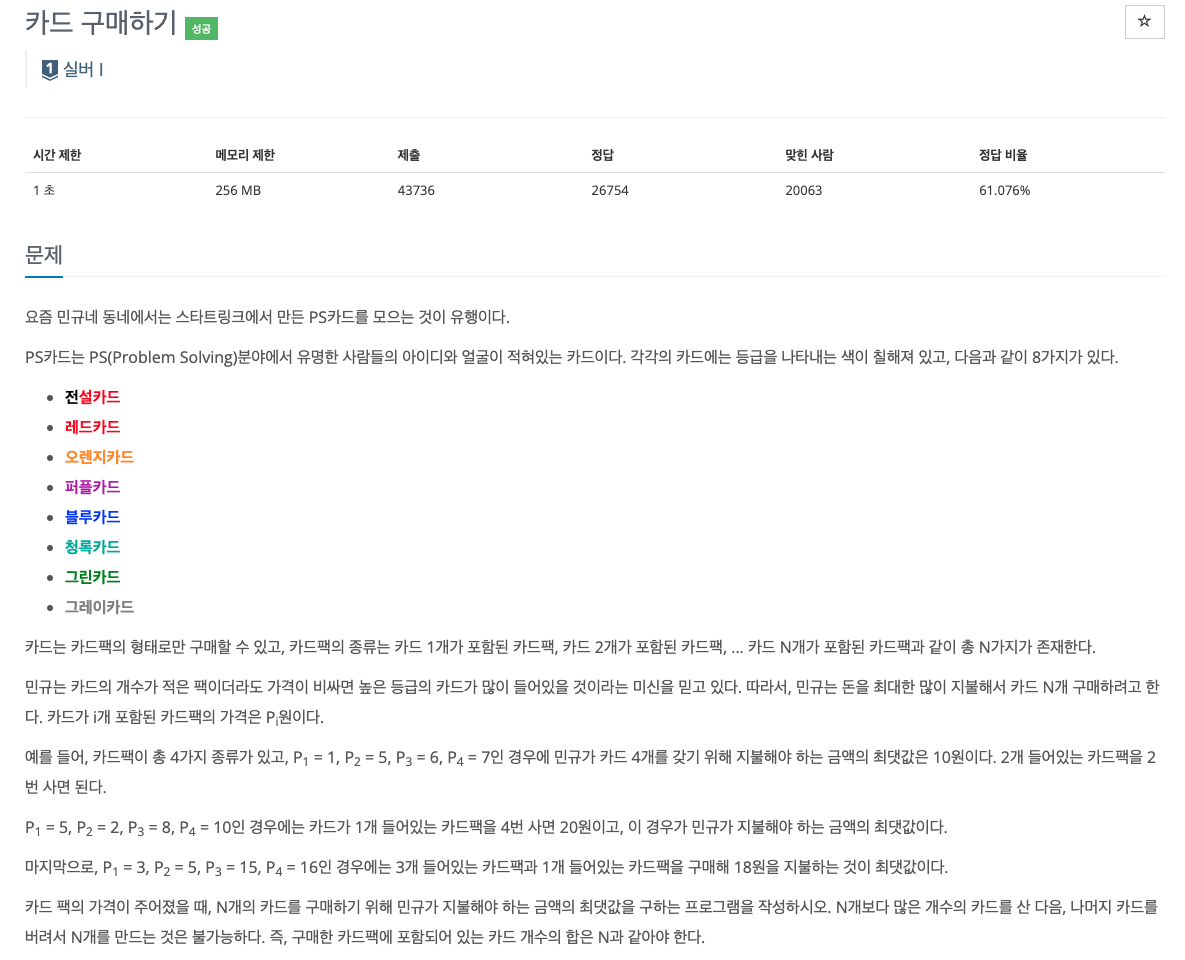
print(dp[n][n])이번 문제는 구매하려고 하는 카드의 개수 N과 각 개수마다 구매하는데 필요한 비용 P1 ~ PN 까지 주어졌을 때, 카드 N개를 최대한 많은 비용으로 구매하였을 때의 금액을 구하는 문제이다.
이 문제를 풀 때 문득 '0-1 배낭 문제'가 떠올랐는데, 비슷한 느낌으로 풀 수 있었던 것 같다.
먼저 카드의 개수를 세로 값으로, 각 카드의 사용여부를 가로 값으로 지정하여 2차원 리스트(DP 테이블)을 선언하고 0으로 초기화 해주었다.
💡 P1 = 5, P2 = 2, P3 = 8, P4 = 10
| 5 | 0 | 0 | 0 |
| 10 | 0 | 0 | |
| 15 | 0 | ||
| 20 |
먼저 1번째 열을 초기 값으로 설정해 준 뒤, 2차원 리스트의 대각선을 기준으로 위에 존재하는 값들은 현재의 카드의 개수보다 많은 값들이기 때문 모두 0으로 설정해주었다.
ex) 1번째 행(n=1)은 2,3,4번째 열(n=2,3,4)보다 카드의 개수가 적기 때문에 구매할 수 X
💡 P1 = 5, P2 = 2, P3 = 8, P4 = 10
| 5 | 0 | 0 | 0 |
| 10 | 0 | 0 | |
| 15 | 0 | ||
| 20 |
초기 값이 설정되고 나면 차례대로 DP 테이블을 채워나가야 하는데, 위 예시에서는 (2,2)를 채우는 기준은 다음과 같다.
👉🏻 (2,2) 값의 의미 ? 현재 구매해야 하는 카드의 개수는 2개이고, P1과 P2만을 가지고 구매한다고 가정했을 때, 지불할 수 있는 최대 비용
💡 P1 = 5, P2 = 2, P3 = 8, P4 = 10
| 5 | 0 | 0 | 0 |
| 10 | 10 | 0 | 0 |
| 15 | 15 | 15 | 0 |
| 20 | 20 | 20 | 20 |
따라서 P2를 사용했을 때의 값(price[j-1] + dp[i-j][i-j]) / P2를 사용하지 않고 이전 카드들만을 가지고 사용했을 때의 값(dp[i][j-1]) 을 비교하여 더 큰 값을 채우면 된다 ! (dp[i][j] = max(price[j-1]+dp[i-j][i-j],dp[i][j-1])
2차원 리스트를 활용한 DP 문제를 다시 한번 풀어봄으로써 다시 한번 DP 알고리즘에 대한 감을 익힐 수 있었던 좋은 문제였다 :)
++ (2023/5/4 수정)
N = int(input())
price = [0] + list(map(int,input().split()))
dp = [0 for _ in range(N+1)]
for i in range(1,N+1):
for k in range(1,i+1):
dp[i] = max(dp[i], dp[i-k] + price[k])
print(dp[i])다른 사람들의 풀이를 확인해보니, 이 문제에서는 고려할 요소가 가격 하나 이기 때문에 2차원 DP 테이블을 만들 필요없이, 1차원 리스트를 만들어서 dp[i] = price[k] + dp[i - k] 라는 점화식으로 간단하게 풀이할 수 있다.
(index를 통일하기 위하여 가격을 저장할 때 [0] + list(map(int,input().split())) 방식으로 저장하는 것도 좋은 방법인 것 같다)
'Algorithm 💡 > DP' 카테고리의 다른 글
| [백준 18353번] 병사 배치하기 (0) | 2023.03.16 |
|---|---|
| [백준 11053번] 가장 긴 증가하는 부분 수열(LIS) (0) | 2023.03.15 |
| [백준 1010번] 다리놓기 (0) | 2023.03.15 |
| [백준 1912번] 연속합 (0) | 2023.03.14 |
| [백준 11726번] 2xn 타일링 (0) | 2023.03.14 |



