

def dynamic(data):
n = data[0]
m = data[1]
dp = [[0]*(m+1) for _ in range(n+1)]
for i in range(1,n+1):
dp[i][i] = 1
for i in range(2,m+1):
dp[1][i] = i
for i in range(2, n+1):
for j in range(i+1,m+1):
dp[i][j] = dp[i-1][j-1] + dp[i][j-1]
print(dp[n][m])
t = int(input())
testcase = []
for i in range(t):
testcase.append(list(map(int,input().split())))
for i in testcase:
dynamic(i)
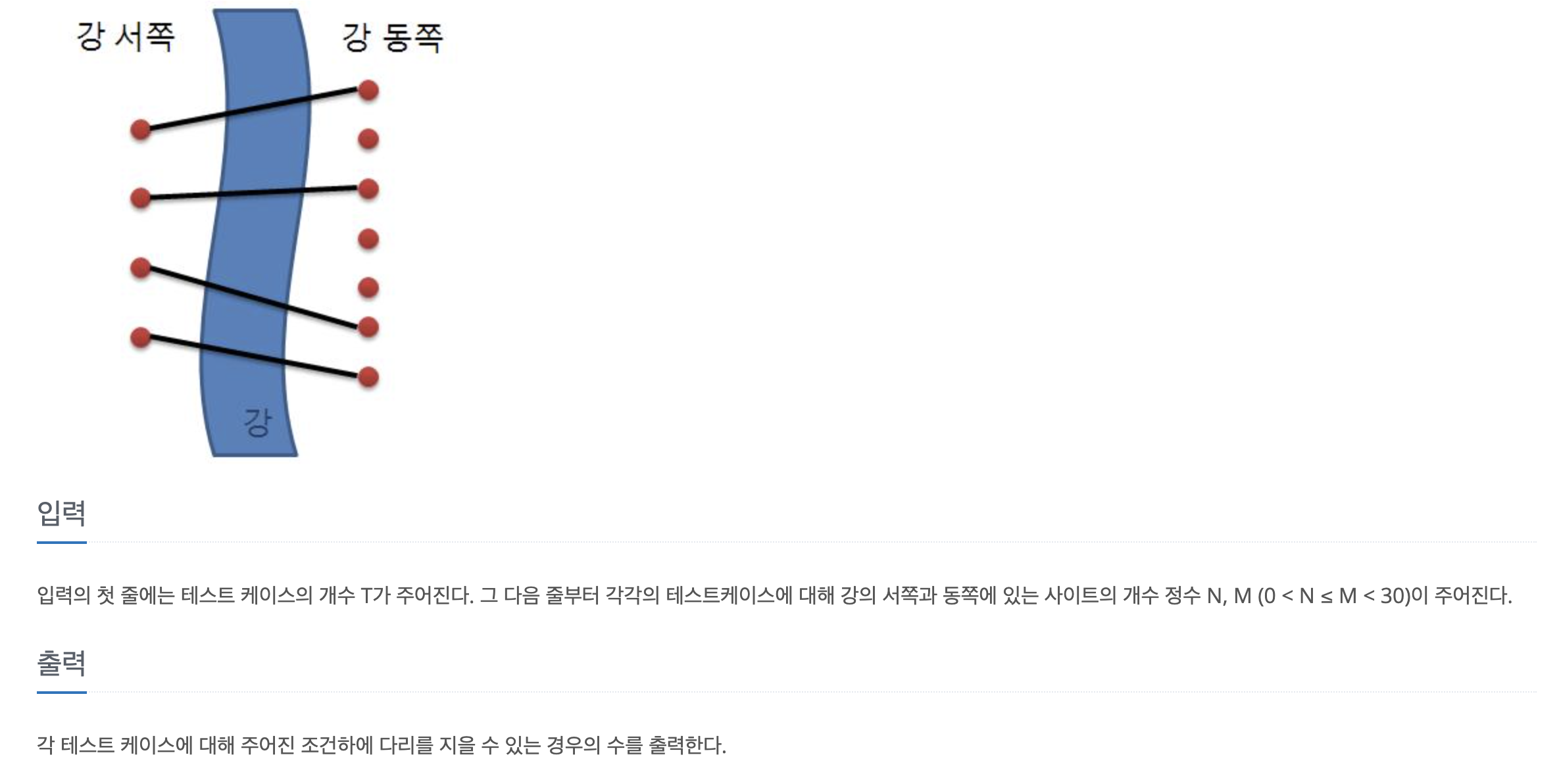
이번 문제는 서쪽 사이트의 개수(n)과 동쪽 사이트의 개수(m)이 주어졌을 때, 다리끼리 서로 겹쳐지지 않으면서 다리를 놓을 수 있는 경우의 수를 구하는 문제이다.
| 1 | 2 | 3 | 4 | 5 |
| 1 | ||||
| 1 | ||||
| 1 |
처음에 문제를 접근할 때 패턴이나 점화식을 1차원으로 찾으려고 했었는데, n과 m이라는 두 개의 값이 주어졌기 때문에 DP 테이블로 2차원 리스트를 선언하고 초기 값을 설정해주었다. (dp[n][n] = 1, dp[1][m] = m)
| 1 | 2 | 3 | 4 | 5 |
| 1 | 3 | 6 | 10 | |
| 1 | 10 | 16 | ||
| 1 | 1 |
그 후에 dp[2][3]부터 차근차근 구해보니 dp[i][j] = dp[i-1][j-1] + dp[i][j-1] 라는 점화식을 얻을 수 있었고, 이를 통해 DP 테이블을 채우면서 값을 구할 수 있었다 :)
'Algorithm 💡 > DP' 카테고리의 다른 글
| [백준 11053번] 가장 긴 증가하는 부분 수열(LIS) (0) | 2023.03.15 |
|---|---|
| [백준 11052번] 카드 구매하기 (0) | 2023.03.15 |
| [백준 1912번] 연속합 (0) | 2023.03.14 |
| [백준 11726번] 2xn 타일링 (1) | 2023.03.14 |
| [백준 1003번] 피보나치 함수 (0) | 2023.03.13 |



