# 1
# 2
# 3 (2 + 1)
# 5 (3 + 2)
# 8 (5 + 3)
# 13 (8 + 5)
n = int(input())
if n == 1:
print(1)
elif n == 2:
print(2)
else:
dp = [0]*(n+1)
dp[1], dp[2] = 1, 2
for i in range(3,n+1):
dp[i] = dp[i-1] + dp[i-2]
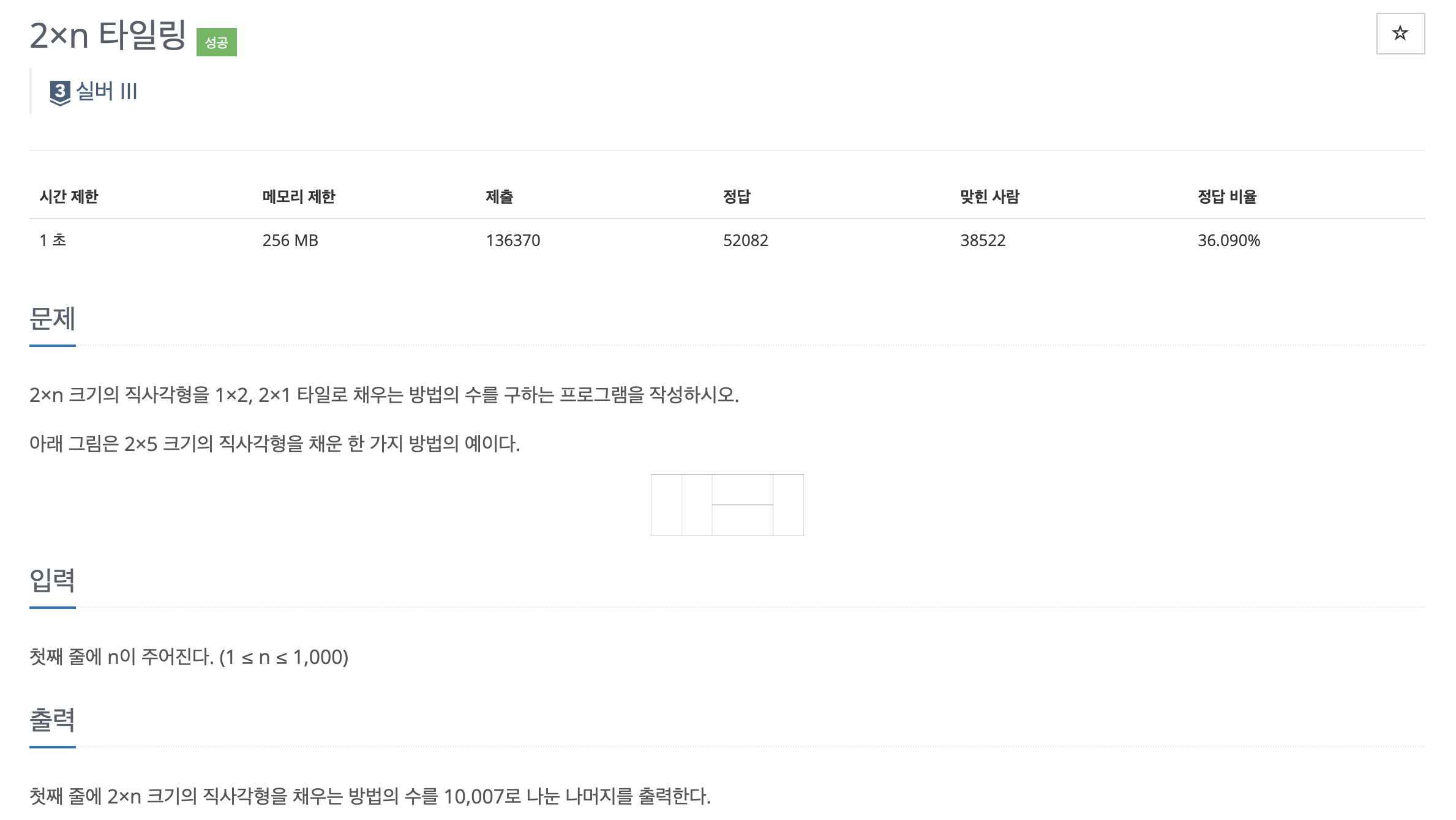
print(dp[n]%10007)이번 문제는 2xn 형태의 직사각형이 주어졌을 때, 2x1과 1x2 타일로 채울 수 있는 경우의 수를 구하는 문제이다.
n=1, n=2, n=3 .. 인 경우의 수를 차례대로 구하다보니 dp[n] = dp[n-1] + dp[n-2] 라는 점화식을 도출해낼 수 있어서 쉽게 해결할 수 있었던 문제였다 :)
'Algorithm 💡 > DP' 카테고리의 다른 글
| [백준 1010번] 다리놓기 (0) | 2023.03.15 |
|---|---|
| [백준 1912번] 연속합 (0) | 2023.03.14 |
| [백준 1003번] 피보나치 함수 (0) | 2023.03.13 |
| [백준 2775번] 부녀회장이 될테야 (0) | 2023.03.13 |
| [백준 9095번] 1, 2, 3 더하기 (1) | 2023.03.10 |



