def dynamic(n):
if n == 1:
return 1
if n == 2:
return 2
if n == 3:
return 4
dp = [0]*(n+1)
dp[1],dp[2],dp[3] = 1, 2, 4
for i in range(4, n+1):
dp[i] = dp[i-1] + dp[i-2] + dp[i-3]
return dp[n]
t = int(input())
result = []
for i in range(t):
n = int(input())
result.append(dynamic(n))
for i in result:
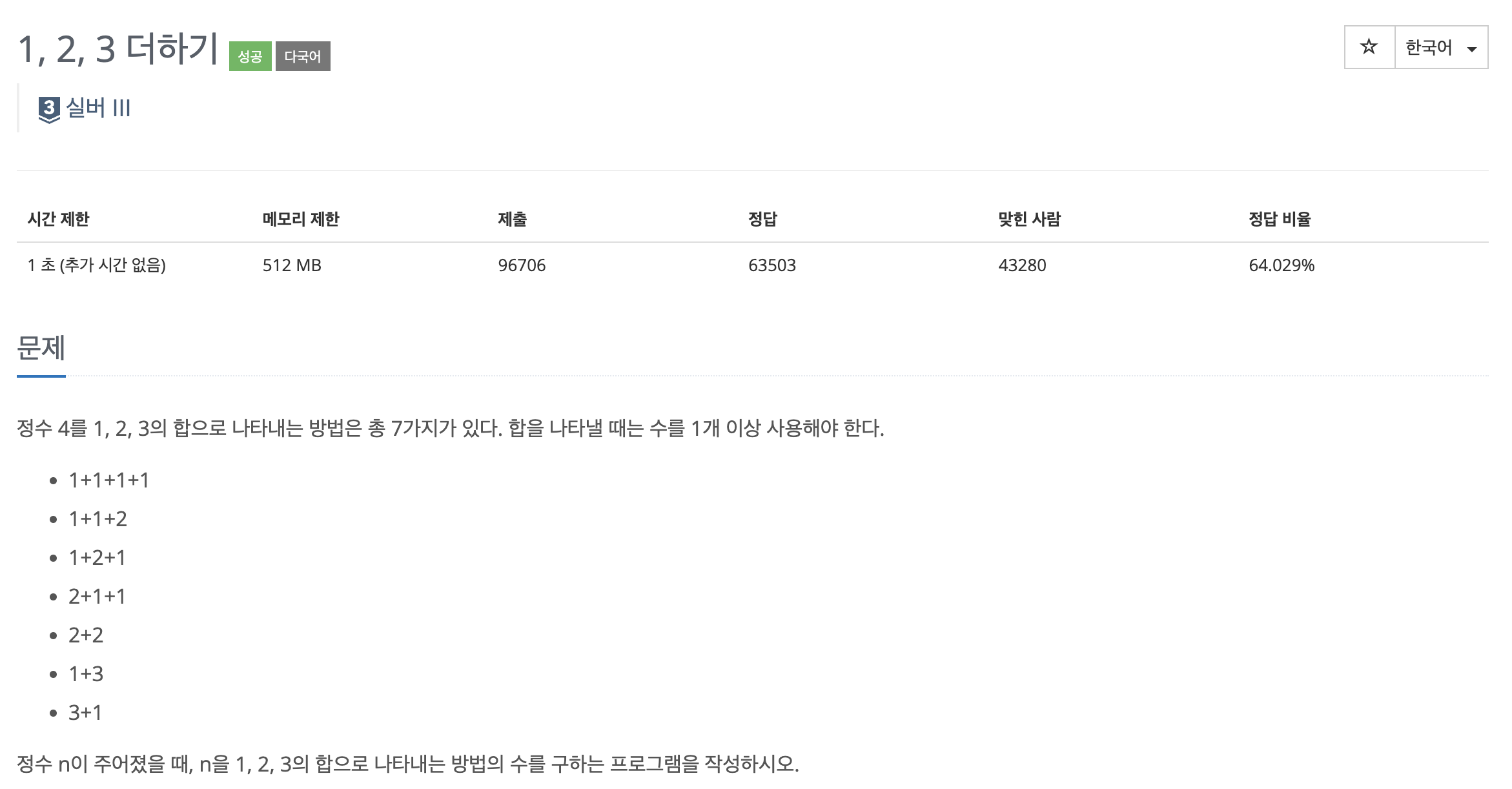
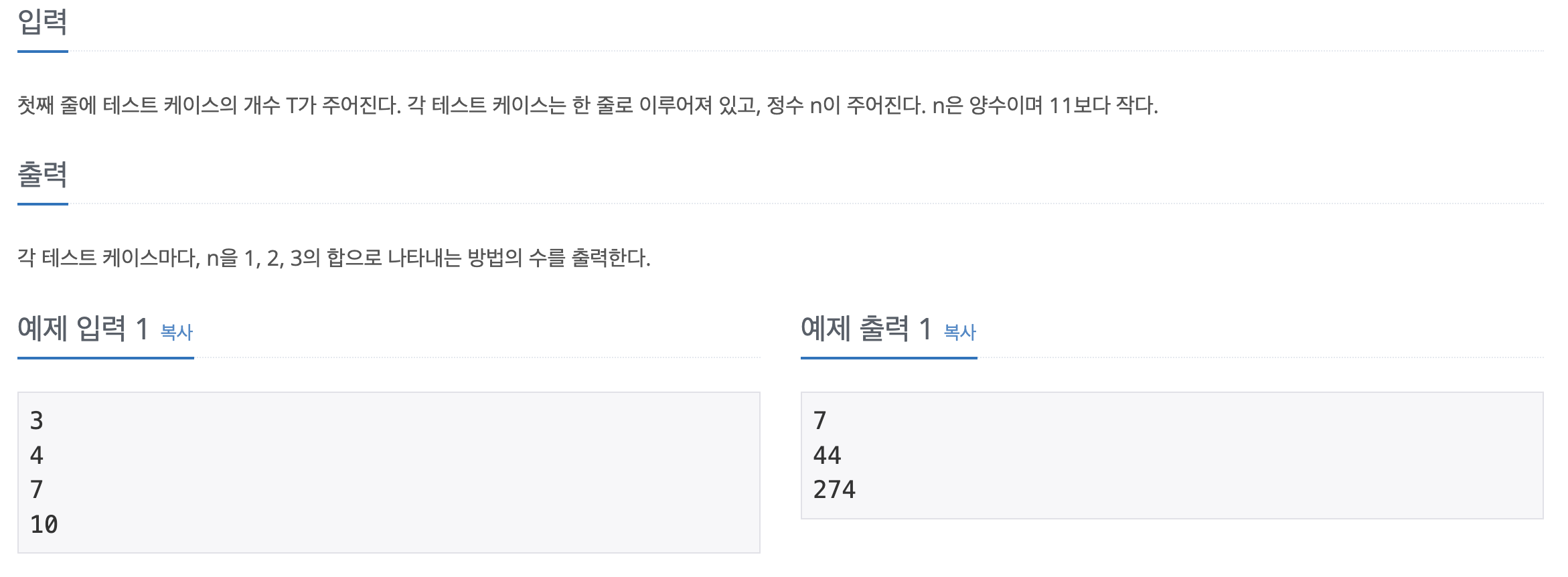
print(i)이번 문제는 주어진 정수 N을 1, 2, 3의 합으로 만들 수 있는 경우의 수를 구하는 문제이다.
n=1, n=2, n=3 인 경우를 DP 테이블에 저장하고 n=4 부터는 dp[n] = dp[n-1] + dp[n-2] + dp[n-3] 이라는 점화식을 도출한 뒤에 풀면 쉽게 답을 구할 수 있다 !
다시 한번 반성하는 것이지만 DP 알고리즘을 풀 때는 번거롭더라도 최소 n=5 까지는 경우의 수를 모두 구해보고 점화식을 도출하거나 패턴을 찾도록 하자 !
'Algorithm 💡 > DP' 카테고리의 다른 글
| [백준 1003번] 피보나치 함수 (0) | 2023.03.13 |
|---|---|
| [백준 2775번] 부녀회장이 될테야 (0) | 2023.03.13 |
| [백준 2156번] 포도주 시식 (0) | 2023.03.08 |
| [백준 12865번] 평범한 배낭 (0) | 2023.03.08 |
| [백준 10844번] 쉬운 계단 수 (0) | 2023.03.07 |



