n = int(input())
weight = [0]*10000
dp = [0]*10000
for i in range(n):
weight[i] = int(input())
dp[0] = weight[0]
dp[1] = weight[0] + weight[1]
dp[2] = max(weight[2]+weight[0], weight[2]+weight[1], dp[1])
for i in range(3,n):
dp[i]=max(weight[i]+dp[i-2], weight[i]+weight[i-1]+dp[i-3],dp[i-1])
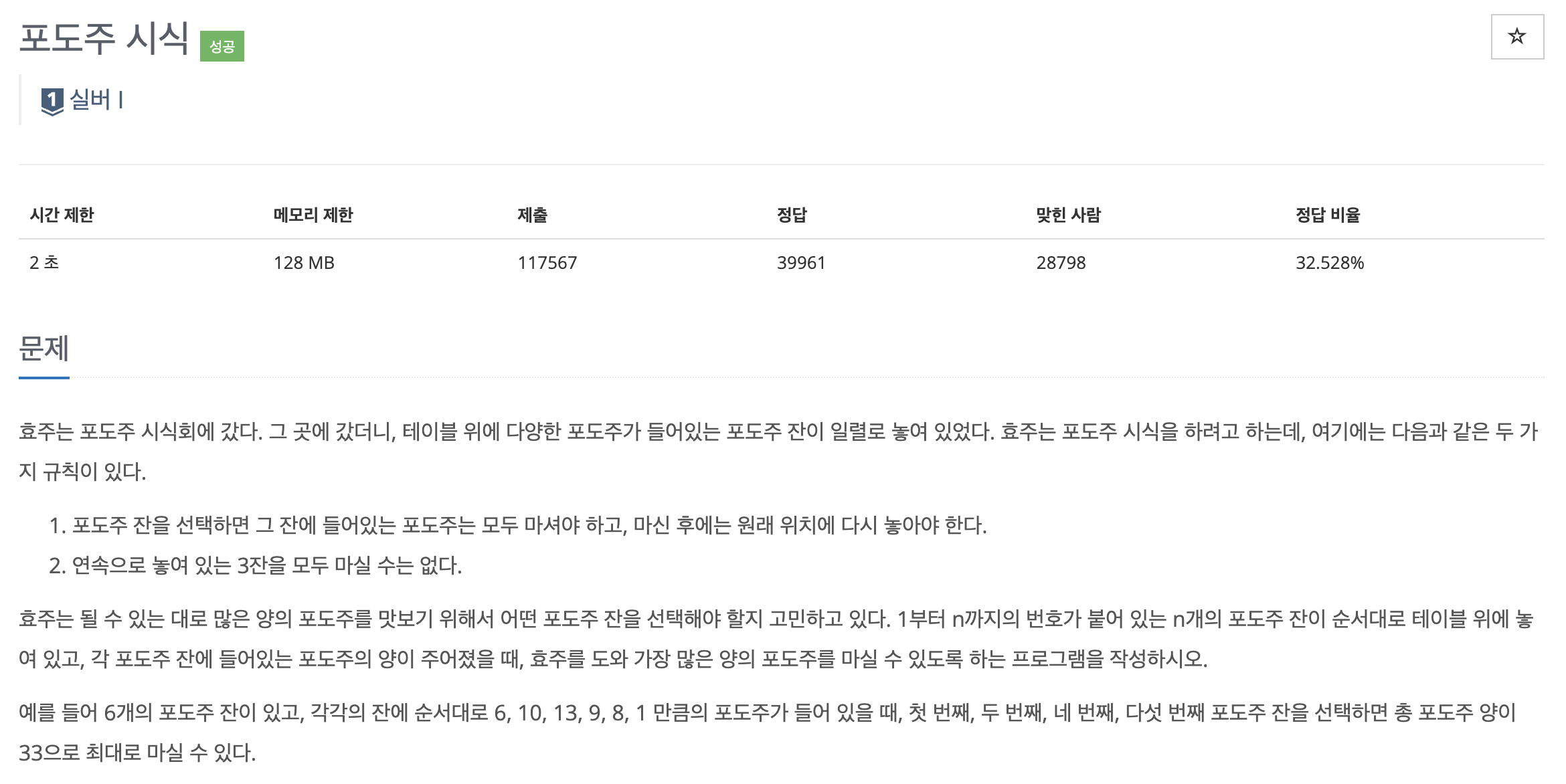
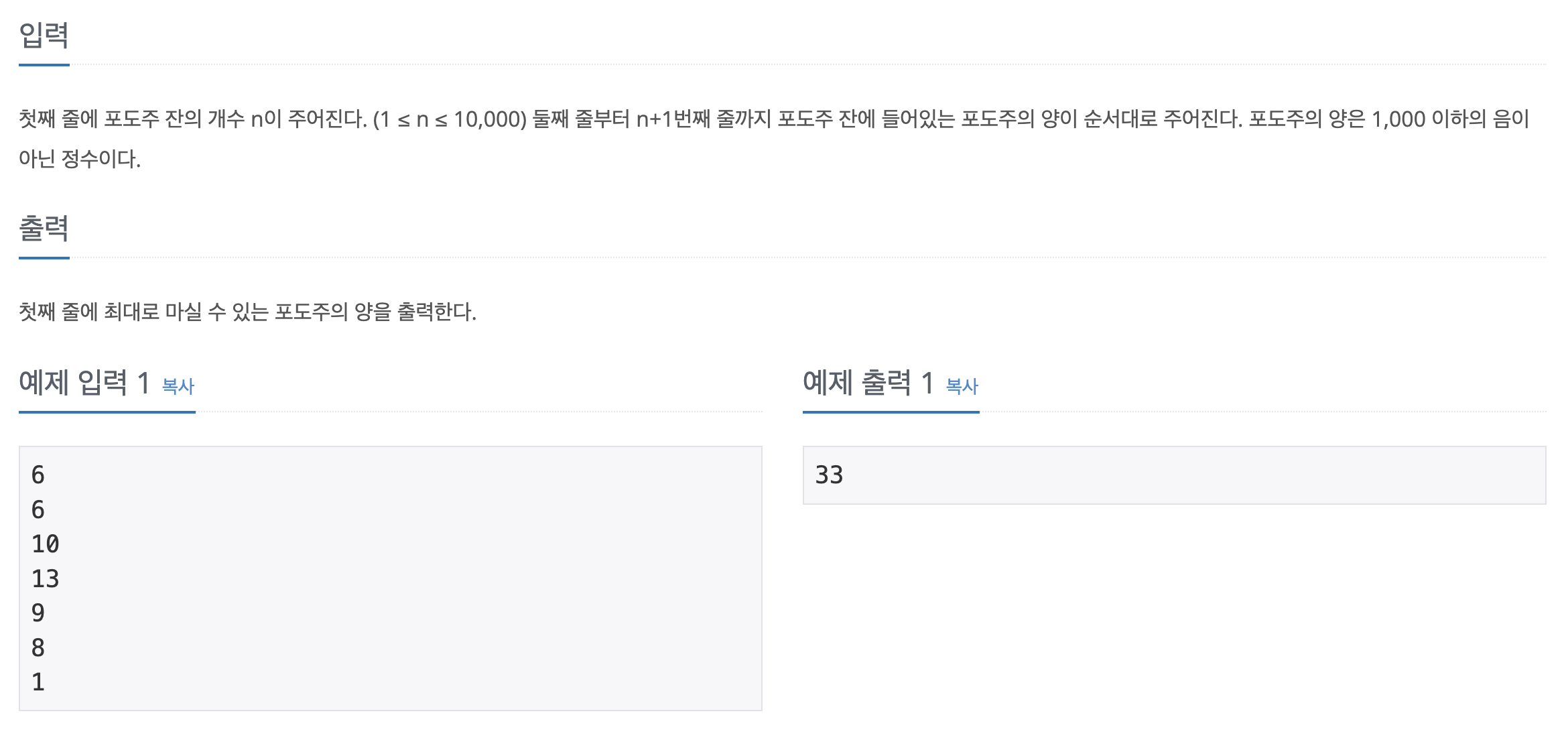
print(max(dp))이번 문제는 이전에 풀었던 '2579번 - 계단 오르기' 문제와 유사한 문제로, 연속 3개의 포도주를 마시지 못한다는 조건 하에 최대로 마실 수 있는 포도주의 양을 구하는 문제이다.
다만, 이전의 계단 오르기 문제와의 차이점은 계단 오르기 문제에서는 마지막 계단을 무조건 밟아야 한다는 조건이 있다는 것이다.
따라서 이 문제에서는
① 현재 포도주와 이전 포도주를 마시고 전전 포두주는 마시지 않는 경우 ( weight[i]+weight[i-1]+dp[i-3] )
② 현재 포도주와 전전 포도주를 마시고 이전 포도주는 마시지 않는 경우 ( weight[i]+dp[i-2] )
③ 현재 포도주를 마시지 않는 경우 ( dp[i-1] )
이 3가지를 고려하여 DP 리스트를 채워나가면 풀 수 있는데, 본인은 3번째 조건을 떠올리지 못하여 성공하지 못하였다.
이번 문제를 통해 느낀 점은 다음과 같다.
1. n이 작은 경우(n=1, n=2, n=3..)를 항상 고려하여 IndexError가 발생하지 않도록 조심하자 !
2. DP 알고리즘을 사용할 때는 무작정 점화식이나 패턴을 찾기 보다는, 모든 경우의 수를 구하는 방법을 먼저 떠올린 후에 작은 값부터 차근차근 DP 리스트에 저장하는 방식으로 풀자.
'Algorithm 💡 > DP' 카테고리의 다른 글
| [백준 2775번] 부녀회장이 될테야 (0) | 2023.03.13 |
|---|---|
| [백준 9095번] 1, 2, 3 더하기 (0) | 2023.03.10 |
| [백준 12865번] 평범한 배낭 (0) | 2023.03.08 |
| [백준 10844번] 쉬운 계단 수 (0) | 2023.03.07 |
| [백준 2579번] 계단 오르기 (0) | 2023.03.05 |



