n, k = map(int,input().split())
list = [(0,0)]
for i in range(n):
list.append(tuple(map(int,input().split())))
dp = [[0] * (k+1) for _ in range(n+1)]
for i in range(1,n+1):
for j in range(1, k+1):
w = list[i][0]
v = list[i][1]
if j < w:
dp[i][j] = dp[i-1][j]
else:
dp[i][j] = max(dp[i-1][j-w] + v,dp[i-1][j] )
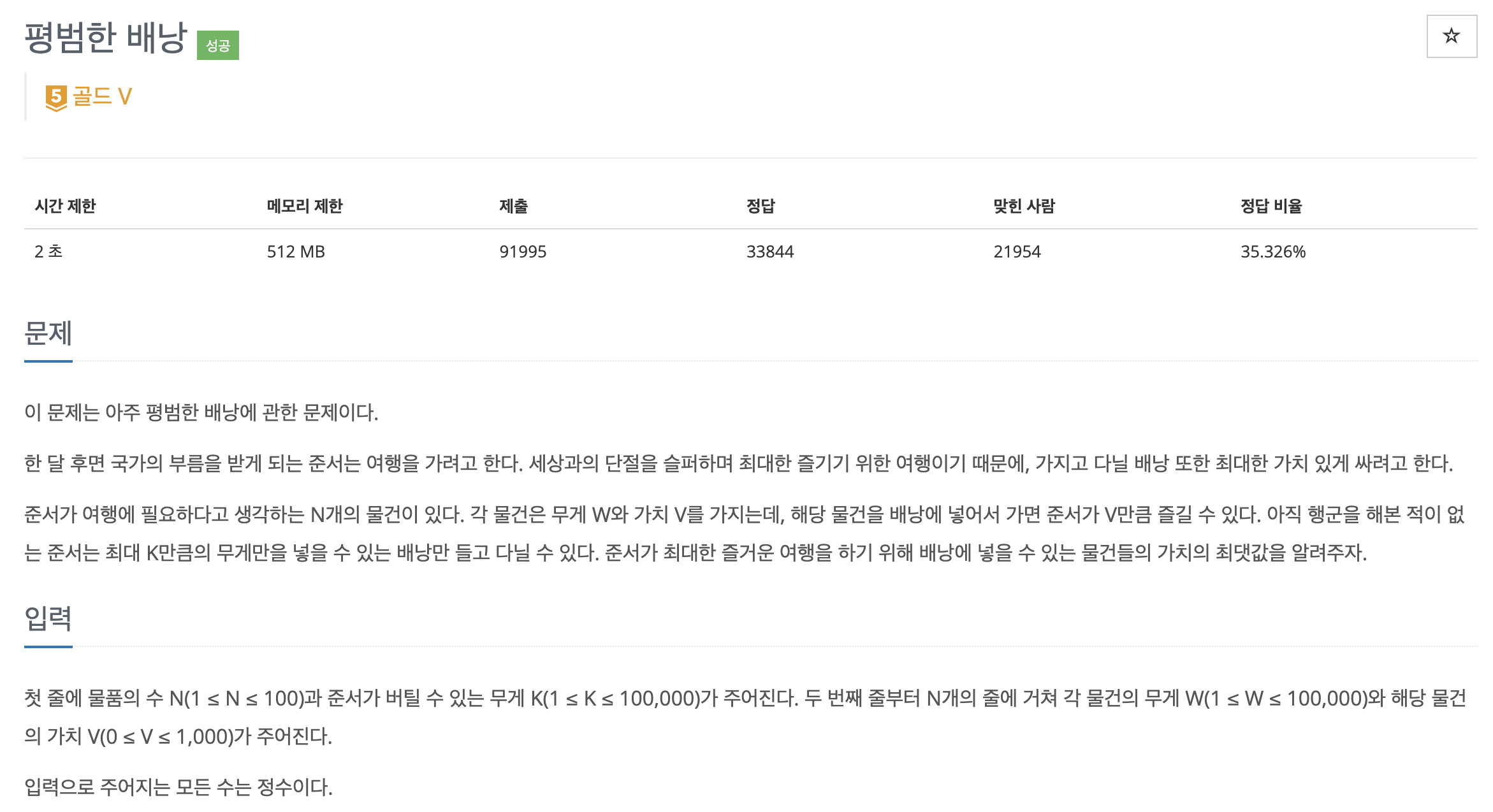
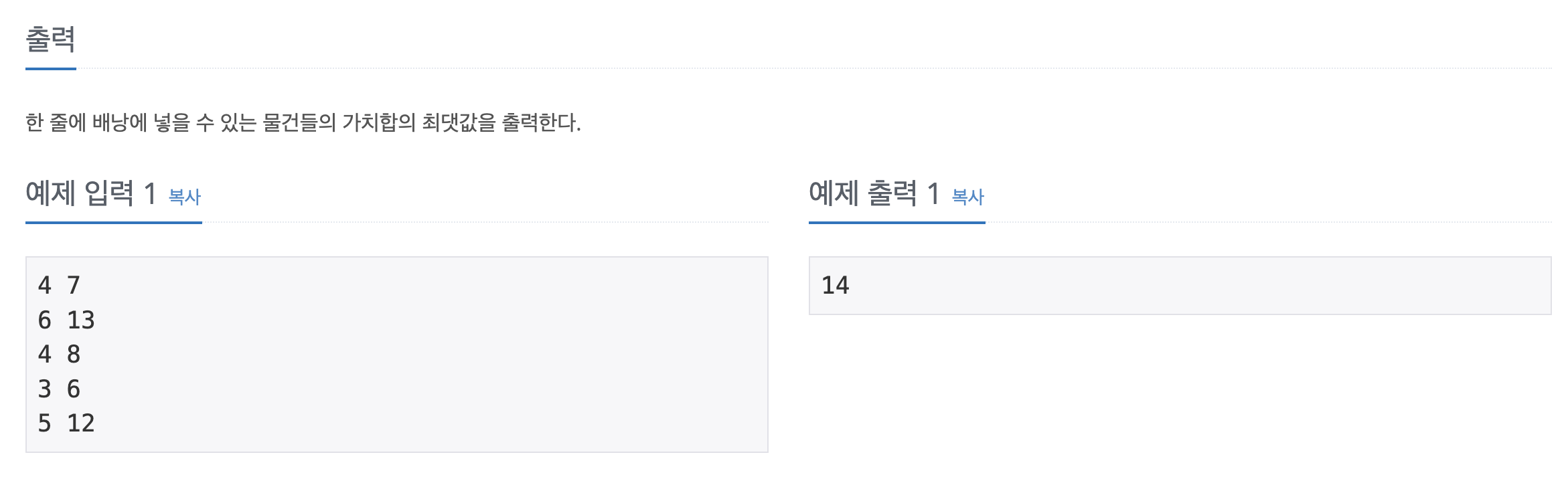
print(dp[n][k])이번 문제는 DP 문제 유형 중 유명한 문제 중 하나로, 최대 무게가 정해진 가방에 무게(w)와 가치(v)가 주어진 물건들을 가지고 가치를 최대화하도록 하는 '0-1 배낭 문제'이다.
이 문제를 처음 접했을 때는 DP 리스트를 무게(w)만 고려하여 1차원으로 선언 및 초기화하여 문제를 풀이하였는데, 이렇게 풀이하다보니 여러가지 오류가 발생하여 다른 사람들의 풀이를 참고하게 되었다.
먼저 이 문제가 왜 DP를 사용하여야 하는지 알아보도록 하자.
1. 만약에 완전 탐색(Brute Force)를 사용하여 풀 경우, 모든 물건들을 배낭에 넣거나/넣지 않거나를 모두 고려하게 되므로 이 알고리즘의 시간 복잡도는 부분 집합의 개수인 O(2^n)이 되기 때문에 주어진 시간 내에 풀이할 수 없다.
2. 큰 문제를 작은 문제들의 합으로 풀이할 수 있다.
ex) AB를 사용하여 만들 수 있는 최대 값 = max(A를 사용하여 만들 수 있는 최대 값 + B 사용, A를 사용하여 만들 수 있는 최대 값 + B 비사용)
👉🏻 하나의 물건을 넣을 때마다 해당 물건까지 넣었을 때 가질 수 있는 최대 값을 저장(유지)하며 풀이할 수 있다 !
따라서 세로축을 물건의 개수(n)으로, 가로축을 가방의 최대 무게(k)로 DP 리스트를 선언 및 초기화하고,
각 물건을 담을지 말지 결정할 때 마다 현재 담을 수 있는 무게(k)가 해당 물건의 무게(w)보다 작은 경우에는 넣지 않고, 같거나 큰 경우에는 해당 물건의 넣어서 2가지 경우 중 큰 값을 저장한다.
DP 문제를 풀이할 때 큰 문제를 해결하기 위해 어떤 값들을 고려하고 저장해야 하는지 다시 한번 생각해볼 수 있는 문제였다 :)
'Algorithm 💡 > DP' 카테고리의 다른 글
| [백준 9095번] 1, 2, 3 더하기 (0) | 2023.03.10 |
|---|---|
| [백준 2156번] 포도주 시식 (0) | 2023.03.08 |
| [백준 10844번] 쉬운 계단 수 (0) | 2023.03.07 |
| [백준 2579번] 계단 오르기 (0) | 2023.03.05 |
| [백준 1149번] RGB거리 (0) | 2023.03.05 |



