
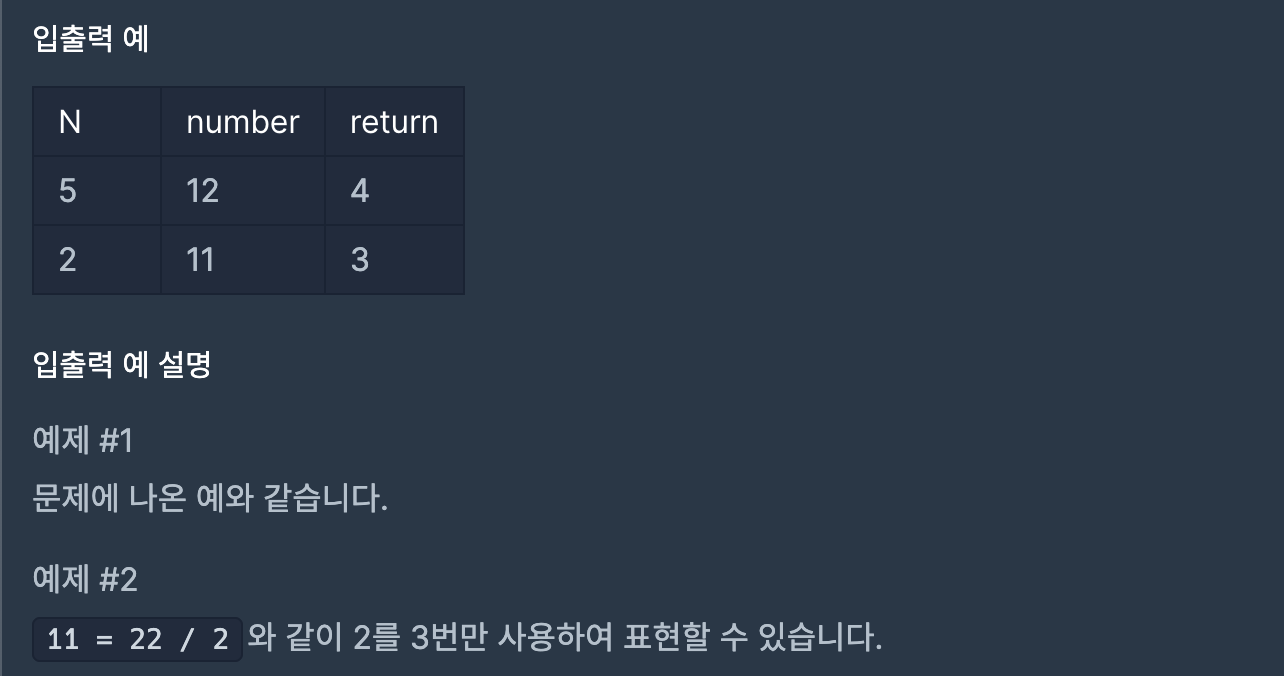
def solution(N, number):
answer = -1
if N == number:
return 1
# N을 i+1번 사용했을 때 만들 수 있는 값들
dp = [set() for i in range(9)]
for i in range(1,9):
dp[i].add(int(str(N)*i))
for i in range(2,9):
for j in range(1,i):
for term1 in dp[j]:
for term2 in dp[i-j]:
dp[i].add(term1 + term2)
dp[i].add(term1 - term2)
dp[i].add(term1 * term2)
if term2 != 0:
dp[i].add(term1 // term2)
if number in dp[i]:
return i
return answer
본 문제는 숫자 N과 number가 주어질 때, N과 사칙연산만 사용해서 number를 표현할 수 있는 N의 최소 사용 횟수를 구하는 문제이다.
솔직하게 이 문제는 유형을 이미 알고 시작해서 DP로 풀이해야겠다고 생각은 했는데, 생각보다 규칙을 찾기가 어려워서 다른 사람의 풀이를 참고하였다.
일단 먼저 사용 횟수가 1개인 경우부터 2개인 경우, 3개인 경우를 구해보면 다음과 같다.
- 1개로 만들 수 있는 수의 집합 :
- 5
- 2개로 만들 수 있는 수의 집합 :
- 55
- [1개로 만들 수 있는 수의 집합] * [1개로 만들 수 있는 수의 집합]
- (5)+5, (5)-5, (5)*5, (5)//5
- [1개로 만들 수 있는 수의 집합] * [1개로 만들 수 있는 수의 집합]
- 5+(5), 5-(5), 5*(5), 5//(5)
- 3개로 만들 수 있는 수의 집합 :
- 555
- [1개로 만들 수 있는 수의 집합] * [2개로 만들 수 있는 수의 집합]
- 5+(55), 5-(55), 5*(55), 5//(55)
- 5+(5+5), 5-(5+5), 5*(5+5), 5//(5+5)
- 5+(5-5), 5-(5-5), 5*(5-5), 5//(5-5)
- 5+(55), 5-(55), 5*(55), 5//(55)
- 5+(5//5), 5-(5//5), 5*(5//5), 5//(5//5)
- [2개로 만들 수 있는 수의 집합] * [1개로 만들 수 있는 수의 집합]
- (55)+5, (55)-5, (55)*5, (55)//5
- (5+5)+5, (5+5)-5, (5+5)*5, (5+5)//5
- (5-5)+5, (5-5)-5, (5-5)*5, (5-5)//5
- (55)+5, (55)-5, (5*5)5, (55)//5
- (5//5)+5, (5//5)-5, (5//5)*5, (5//5)//5
- 4개로 만들 수 있는 수의 집합 :
- 5555
- [1개로 만들 수 있는 수의 집합] * [3개로 만들 수 있는 수의 집합]
- [2개로 만들 수 있는 수의 집합] * [2개로 만들 수 있는 수의 집합]
- [3개로 만들 수 있는 수의 집합] * [1개로 만들 수 있는 수의 집합]
- …
위 결과들을 확인해보면
(n개를 사용해서 만들 수 있는 수의 집합) =
(1개를 사용해서 만들 수 있는 수의 집합) * (n-1개를 사용해서 만들 수 있는 수의 집합) +
(2개를 사용해서 만들 수 있는 수의 집합) * (n-2개를 사용해서 만들 수 있는 수의 집합) + …
라는 규칙성을 가지게 되고, 이를 통해 작은 문제에서 구한 정답들로 그것을 포함하는 더 큰 문제의 정답을 구할 수 있다는 것을 확인할 수 있다.
또한 n이 커질수록 중복되는 연산 값들이 많아지기 때문에 ‘한번 계산한 기존의 연산 결과를 재활용’하는 DP를 활용하게 된다면 연산 횟수가 비약적으로 줄어들게 될 것이다.
1. DP테이블 선언
# N을 i+1번 사용했을 때 만들 수 있는 값들
dp = [set() for i in range(9)]
먼저 DP를 사용하기 위해서는 재활용할 값들을 저장할 만한 DP 테이블이 필요하다.(본 문제에서는 사용 횟수가 8이 넘어가면 -1을 리턴하라는 조건이 있기 때문에 길이를 8로 제한한다.)
2. DP테이블 초기값 설정 및 초기화
for i in range(1,9):
dp[i].add(int(str(N)*i))이후에 DP테이블의 초기 값을 설정해주어야 하는데, 본 문제에서 주어진 사칙연산이 아니라 단순히 숫자를 이어 붙인 경우를 넣어주면 된다.
3. 점화식 작성 ⭐️
for i in range(2,9):
for j in range(1,i):
for term1 in dp[j]:
for term2 in dp[i-j]:
dp[i].add(term1 + term2)
dp[i].add(term1 - term2)
dp[i].add(term1 * term2)
if term2 != 0:
dp[i].add(term1 // term2)
(n개를 사용해서 만들 수 있는 수의 집합) =
(1개를 사용해서 만들 수 있는 수의 집합) * (n-1개를 사용해서 만들 수 있는 수의 집합) +
(2개를 사용해서 만들 수 있는 수의 집합) * (n-2개를 사용해서 만들 수 있는 수의 집합) + …
마지막으로 점화식이다. 위 규칙처럼 2개부터 8개(i개)까지 만들 수 있는 수의 집합을 만들기 위해 j개와 i-j개로 만들 수 있는 모든 경우들을 2중 반목문을 통해 더해주는 것이다.
이때 사칙연산의 결과를 집합 자료형에 add 해주고, 나눗셈의 경우에는 나누는 수가 0이 되지 않도록 조건문을 걸어준다.
이렇게 i개로 만들 수 있는 모든 경우의 수를 구한 뒤에, 해당 집합에 number가 존재하면 i+1을 반환하였고, 모든 반복문이 끝날 때까지 존재하지 않는다면 -1을 리턴해주면 된다.
DP에 대한 개념을 다시 상기시켜볼 수 있었던 문제였다 :)
'Algorithm 💡 > DP' 카테고리의 다른 글
| [백준 15989번] 1, 2, 3 더하기 4 (1) | 2024.09.26 |
|---|---|
| [프로그래머스 Lv.3] 등굣길 (0) | 2024.07.15 |
| [백준 2096번] 내려가기 (0) | 2024.06.28 |
| [백준 17404번] RGB거리 2 (0) | 2023.10.01 |
| [백준 11659번] 구간 합 구하기 4 (0) | 2023.10.01 |



