17404번: RGB거리 2
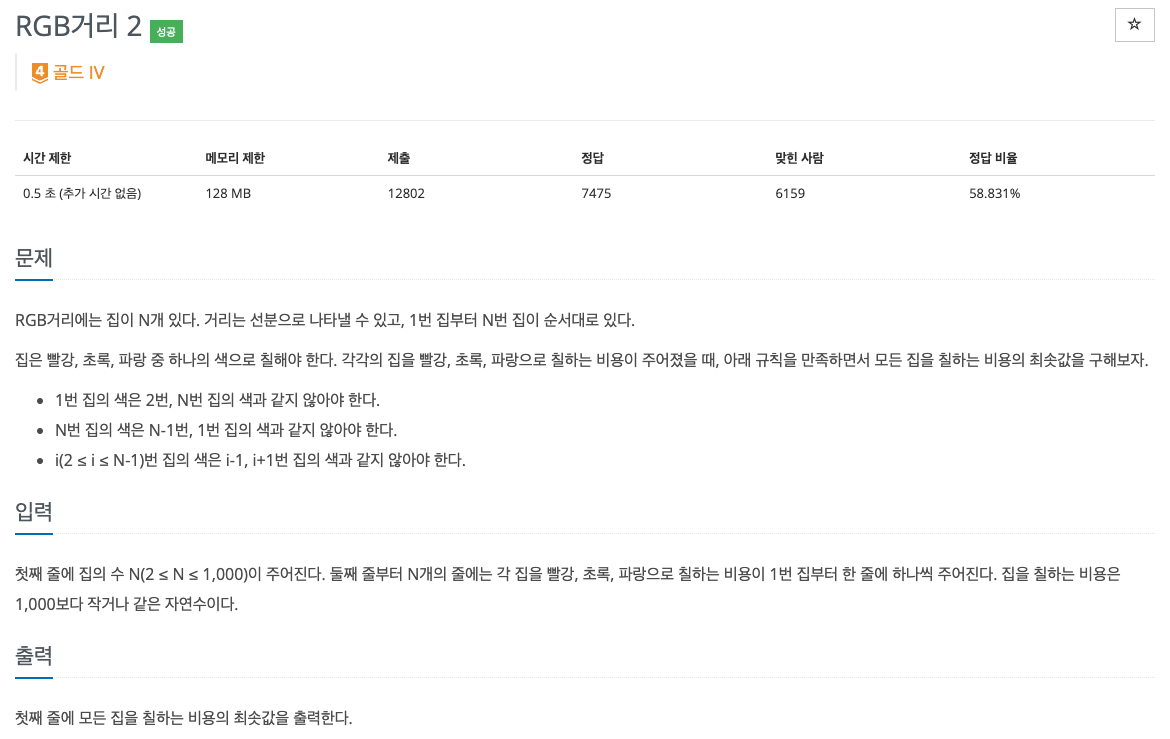
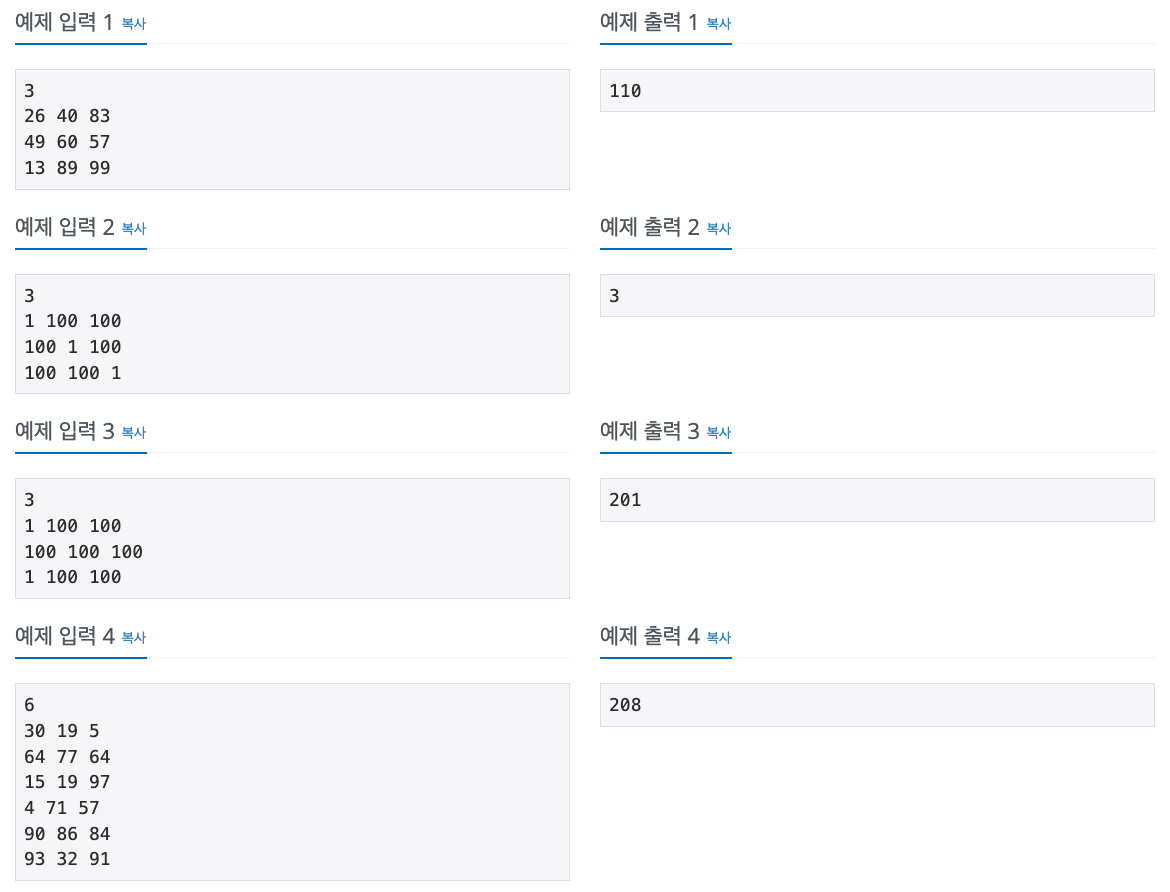
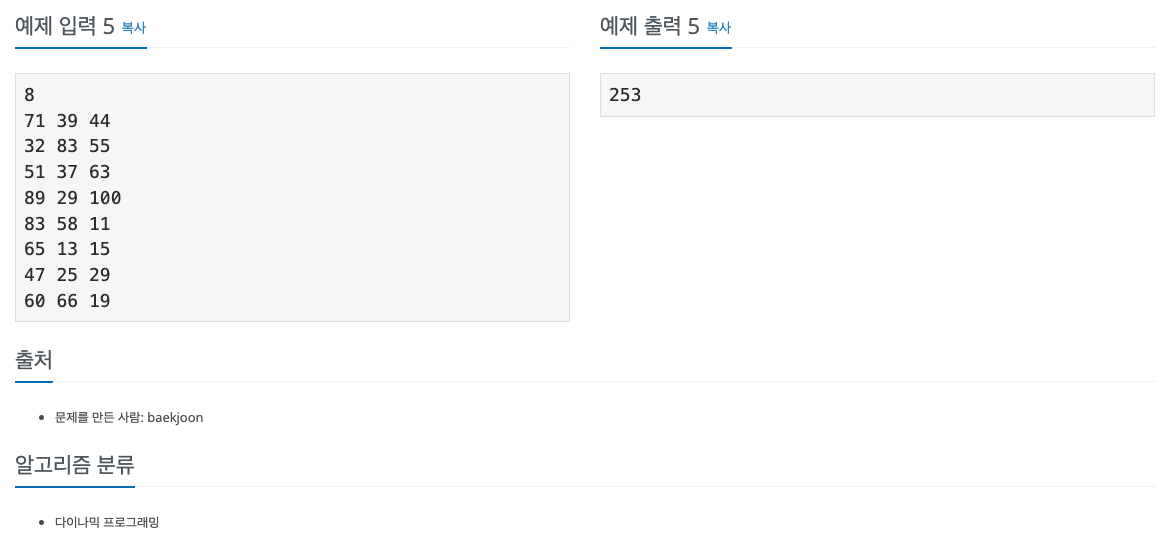
첫째 줄에 집의 수 N(2 ≤ N ≤ 1,000)이 주어진다. 둘째 줄부터 N개의 줄에는 각 집을 빨강, 초록, 파랑으로 칠하는 비용이 1번 집부터 한 줄에 하나씩 주어진다. 집을 칠하는 비용은 1,000보다 작거나
www.acmicpc.net
n = int(input())
costs = [list(map(int,input().split())) for _ in range(n)]
answer = float("inf")
for i in range(3):
dp = [[float("inf")]*3 for _ in range(n+1)]
dp[0][i] = costs[0][i]
for j in range(1,n):
dp[j][0] = min(dp[j-1][1],dp[j-1][2]) + costs[j][0]
dp[j][1] = min(dp[j-1][0],dp[j-1][2]) + costs[j][1]
dp[j][2] = min(dp[j-1][0],dp[j-1][1]) + costs[j][2]
for j in range(3):
if i != j:
answer = min(answer,dp[n-1][j])
print(answer)이번 문제는 RGB거리 문제의 후속 편인 문제로, 지난 문제와 다르게 바로 '양 옆의 집과 색깔이 서로 달라야 하는 조건'에 더불어 '첫번째 집과 N번째 집의 색깔이 달라야 하는 조건'까지 추가된 문제다.
분명 DP 알고리즘을 사용해야 한다는 것을 인지하고, 초기값을 설정해주려고 하는데 첫번째와 N번째를 다르게 설정해야 한다는 제약조건을 만족시키는 아이디어가 떠오르지 않았다.
3차원 배열을 선언하기에는 부담이 너무 크고, 더이상 아이디어가 떠오르지 않자 다른 분의 풀이를 참고하게 되었다.
그 결과 아주 획기적인 아이디어를 발견했는데, 첫번째와 N번째 모두 고려하기 까다롭다면 "1가지 집의 색깔을 고정"시키는 것이다 !
따라서 반복문을 사용하여 색깔 하나씩 고정을 시킨 뒤에, 나머지는 이전에 풀었던 DP방식으로 테이블을 채워나가면 된다. 그 후 마지막 n-1번째 행 중에서 고정시킨 색깔과 다른 색깔(i != j)중에서 최솟값을 갱신시켜주면 된다 :)
배운 점 및 느낀 점
- 문제에서 동시에 고려해야 할 조건이 2가지라면, 하나를 고정시키면 나머지를 풀이할 수 있게 된다.
- DP 테이블을 초기화하거나 초기값을 설정할 때 값을 올바르게 설정하도록 하자.
'Algorithm 💡 > DP' 카테고리의 다른 글
| [프로그래머스 Lv.3] N으로 표현 (0) | 2024.07.04 |
|---|---|
| [백준 2096번] 내려가기 (0) | 2024.06.28 |
| [백준 11659번] 구간 합 구하기 4 (0) | 2023.10.01 |
| [백준 2579번] 계단 오르기 (1) | 2023.10.01 |
| [백준 7570번] 줄 세우기 (0) | 2023.08.14 |



