
17471번: 게리맨더링
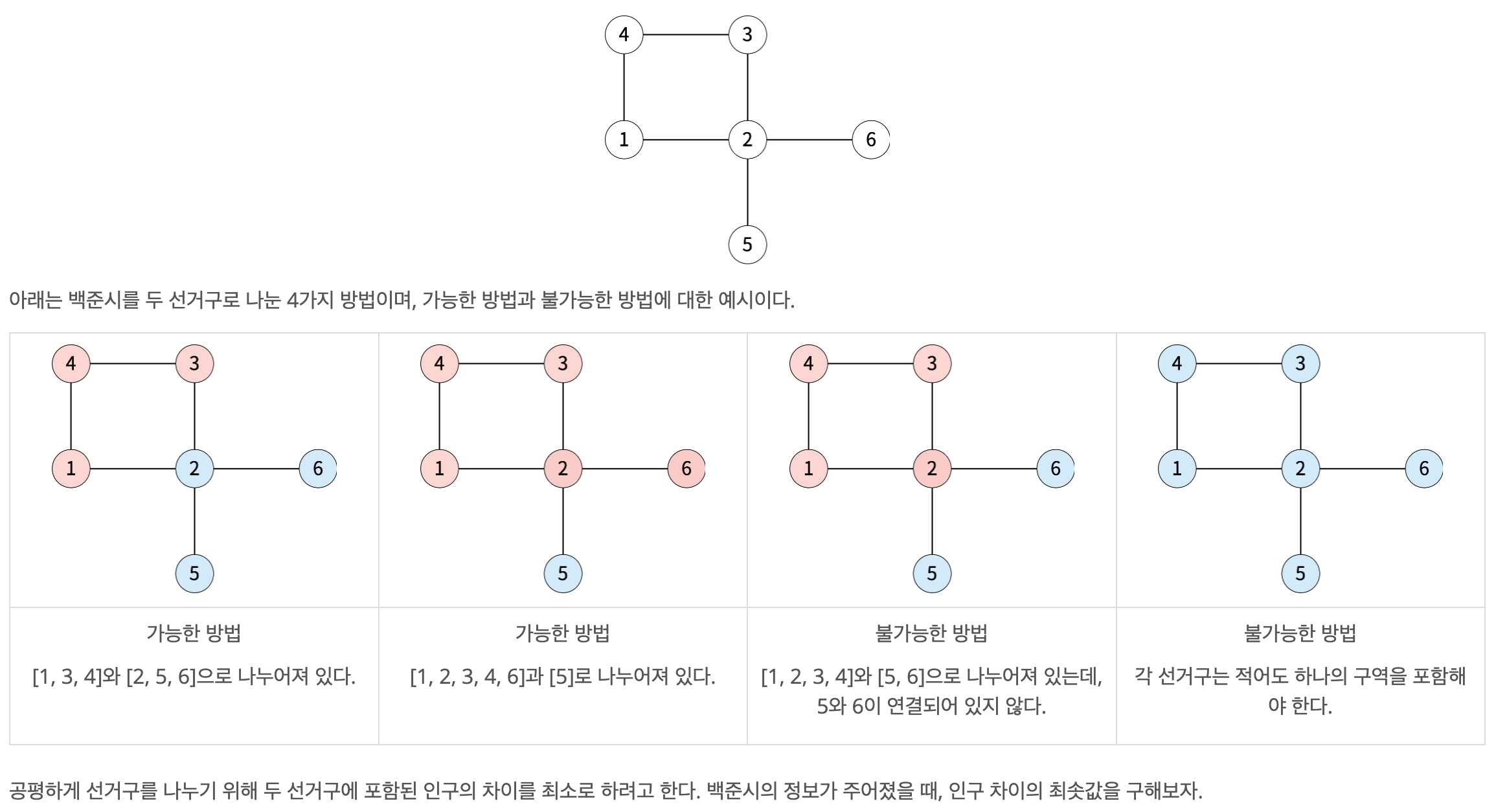
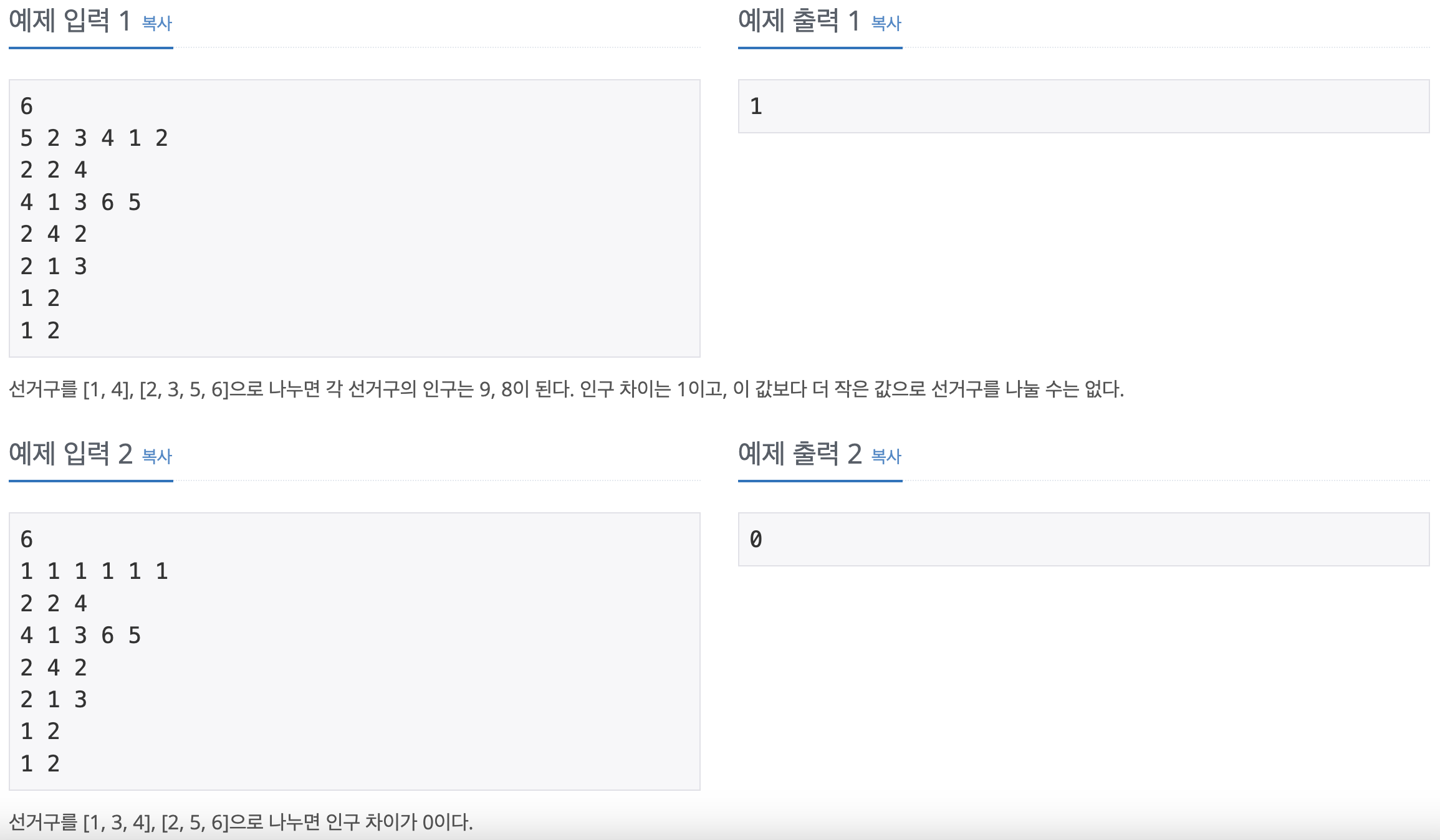
선거구를 [1, 4], [2, 3, 5, 6]으로 나누면 각 선거구의 인구는 9, 8이 된다. 인구 차이는 1이고, 이 값보다 더 작은 값으로 선거구를 나눌 수는 없다.
www.acmicpc.net
import sys
from itertools import combinations
from collections import deque
# 구역을 두 개의 선거구로 나눠야 하고, 각 구역은 두 선거구 중 하나에 포함되어야 한다.
# 선거구는 구역을 적어도 하나 포함해야 하고, 한 선거구에 포함되어 있는 구역은 모두 연결되어 있어야 한다.
input = sys.stdin.readline
n = int(input())
peoples = [0] + list(map(int,input().split()))
graph = [set() for _ in range(n+1)]
answer = float("inf")
visited_set = set()
def bfs(n,s): # 주어진 원소(n)에서 시작하여 방문한 원소들을 반환하는 함수
queue = deque([])
queue.append(n)
visited_set.add(n)
while queue:
v = queue.popleft()
for i in graph[v]:
if i not in visited_set and i in s: # 다음 원소가 주어진 집합(s)에 존재하고, 방문하지 않았을 경우 방문처리
queue.append(i)
visited_set.add(i)
return visited_set
def check(li): # 주어진 원소 집합이 각각 연결되어있는지 확인하는 함수(둘다 연결되어있으면 답 최신화)
global answer
global visited_set
remain = list(set([i for i in range(1,n+1)]) - set(li))
if (bfs(remain[0],set(remain)) & set(remain) == set(remain)) and (bfs(li[0],set(li)) & set(li) == set(li)):
answer = min(answer, abs(sum([peoples[i] for i in remain])-sum([peoples[i] for i in li])))
visited_set = set()
for i in range(n):
neighbors = list(map(int,input().split()))
for j in range(1,len(neighbors)):
graph[i+1].add(neighbors[j])
for i in range(1,n//2+1):
cases = list(combinations([i for i in range(1,n+1)], i))
for c in cases:
check(c)
if answer == float("inf"): # 두 선거구로 나눌 수 없는 경우
print(-1)
else:
print(answer)이번 문제는 주어진 그래프를 2개의 연결된 그래프로 분할했을 때, 각 그래프 원소의 합의 차이의 최솟값을 구하는 문제이다.
처음에 보자마자 완전탐색인건 눈치챘는데, 어떻게 모든 경우의 수를 구해야 할지 감이 잘 오지 않아 다른 사람의 풀이를 참조한 결과 결국 조합(combinations)을 사용해서 구하는 수 밖에 없었다.
1개 이상의 원소로 이루어진 그래프를 각각 만든 뒤에 두 그래프가 모두 연결되어있는지 확인하는 check() 함수를 구현하였다. (연결 여부는 모든 원소를 방문하였는지 확인하기 위해 BFS를 활용하였다)
배운 점 및 느낀 점
- 완전탐색 문제는 DFS/BFS 알고리즘으로 풀이하거나 순열/조합을 구하여 풀 수 있다.
- 구현이 복잡해보인다고 포기하지말고 구현해야 하는 기능을 먼저 파악하자.
'Algorithm 💡 > BruteForce' 카테고리의 다른 글
| [소프티어 6273번] 택배 마스터 광우 (0) | 2024.06.27 |
|---|---|
| [소프티어 7594번] 나무 조경 (1) | 2024.06.25 |
| [백준 1759번] 암호 만들기 (0) | 2024.01.15 |
| [백준 2529번] 부등호 (0) | 2024.01.15 |
| [백준 14889번] 스타트와 링크(재풀이) (1) | 2024.01.06 |



