

2529번: 부등호
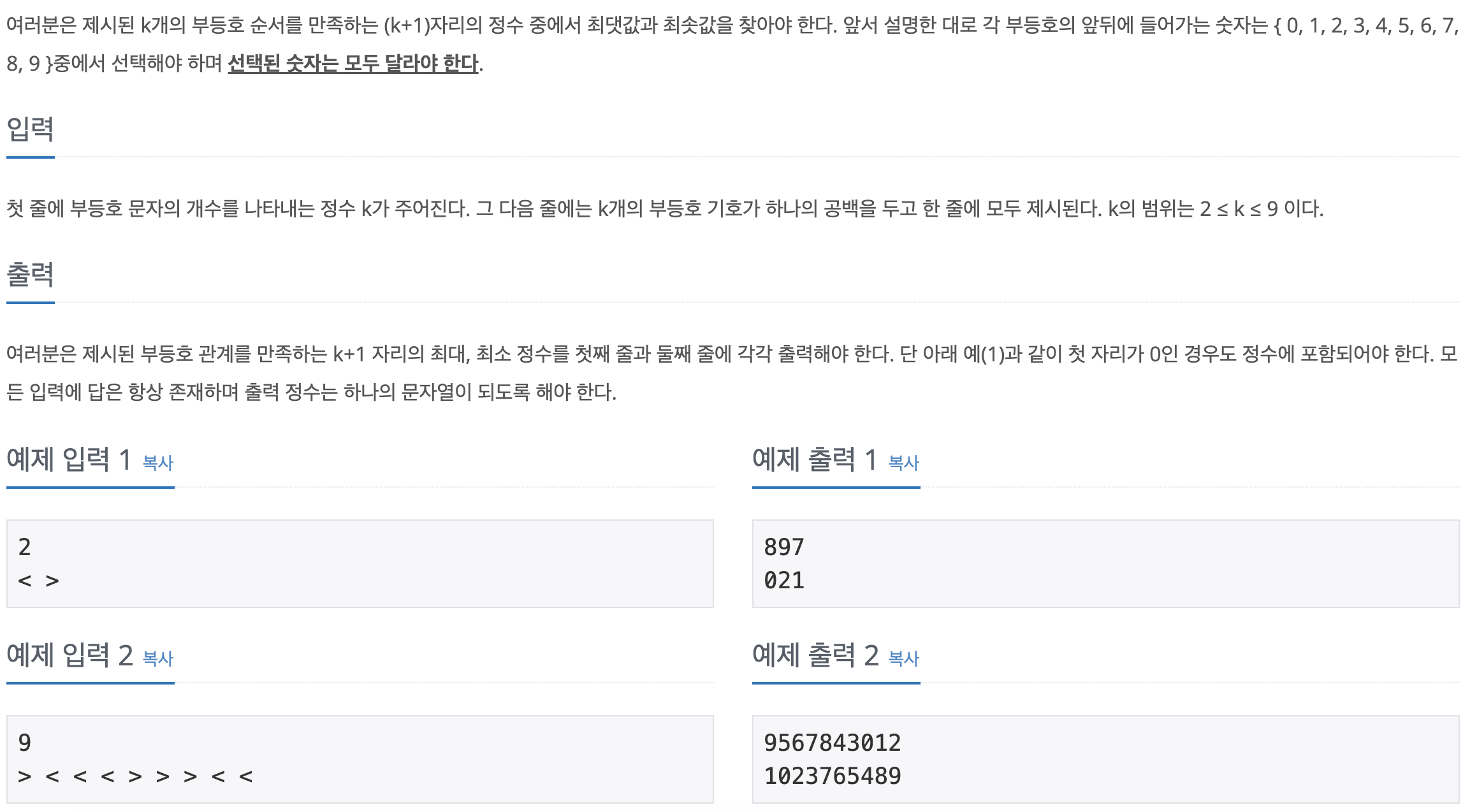
두 종류의 부등호 기호 ‘<’와 ‘>’가 k개 나열된 순서열 A가 있다. 우리는 이 부등호 기호 앞뒤에 서로 다른 한 자릿수 숫자를 넣어서 모든 부등호 관계를 만족시키려고 한다. 예를 들어, 제시
www.acmicpc.net
import copy
k = int(input())
signs = list(input().split())
minimum, maximum = float("inf"), float("-inf")
def dfs(numbers,num_set):
global minimum, maximum, minimum_string, maximum_string
length = len(numbers)
if length == k+1: # 숫자의 개수가 k+1를 만족할 경우 함수 종료
final_value = int("".join(list(map(str,numbers))))
if final_value < minimum:
minimum = final_value
minimum_string = "".join(list(map(str,numbers)))
if final_value > maximum:
maximum = final_value
maximum_string = "".join(list(map(str,numbers)))
return
for num in num_set:
if length == 0: # 첫번째 원소인 경우
new_set = copy.deepcopy(num_set)
new_set.discard(num)
dfs(numbers+[num],new_set)
else: # 부등호에 따라 다르게 탐색
if signs[length-1] == '<' and numbers[length-1] < num:
new_set = copy.deepcopy(num_set)
new_set.discard(num)
dfs(numbers+[num], new_set)
elif signs[length-1] == '>' and numbers[length-1] > num:
new_set = copy.deepcopy(num_set)
new_set.discard(num)
dfs(numbers+[num], new_set)
dfs([], set([0,1,2,3,4,5,6,7,8,9]))
print(maximum_string)
print(minimum_string)
이번 문제는 k개의 부등호가 있을 때, 각 부등호와 숫자 사이의 관계가 만족하도록 하는 k+1개의 숫자 중 최댓값과 최솟값을 구하는 '완전 탐색(Brute-Force)' 문제이다.
dfs 함수를 선언한 뒤, 먼저 종료 조건인 k+1개의 숫자가 주어진 경우 최댓값과 최솟값을 업데이트 해주는 방식으로 코드를 작성하였다. 그 외에는 부등호의 관계에 따라 DFS 함수를 호출하여 모든 경우의 수를 탐색하도록 하였다.
완전 탐색을 연습해볼 수 있었던 문제였다 :)
'Algorithm 💡 > BruteForce' 카테고리의 다른 글
| [백준 17471번] 게리맨더링 (1) | 2024.04.08 |
|---|---|
| [백준 1759번] 암호 만들기 (1) | 2024.01.15 |
| [백준 14889번] 스타트와 링크(재풀이) (1) | 2024.01.06 |
| [프로그래머스] 숫자의 표현 (1) | 2024.01.05 |
| [백준 18808번] 스티커 붙이기 (1) | 2024.01.04 |


