

def solution(maze):
answer = 0
n = len(maze)
m = len(maze[0])
dx = [-1,1,0,0]
dy = [0,0,-1,1]
minimum = float("inf")
is_success = False
# 모든 수레가 각각의 도착 칸에 이동해야 함
# 각 턴 마다 모든 수레를 상하좌우로 인접한 칸 중에 하나로 이동
# 벽(5)이나 격자 판 밖으로 이동 X
# 자신이 방문했던 칸으로 이동 X
# 도착 칸에 위치한 수레는 더 이상 이동 X
# 동시에 두 수레를 같은 칸에 위치 X
# 수레끼리 자리를 바꿀 수 X
for i in range(n):
for j in range(m):
if maze[i][j] == 1:
red_start = (i,j)
if maze[i][j] == 2:
blue_start = (i,j)
if maze[i][j] == 3:
red_end = (i,j)
if maze[i][j] == 4:
blue_end = (i,j)
def get_all_cases(red,blue,visited): # 빨간색 수레와 파란색 수레가 이동할 수 있는 모든 경우의 수를 구하는 함수
x_red, y_red = red
x_blue, y_blue = blue
red_cases = set()
blue_cases = set()
for i in range(4):
nx = x_red + dx[i]
ny = y_red + dy[i]
if 0 <= nx < n and 0 <= ny < m and maze[nx][ny] !=5 and (nx,ny) not in visited[0]:
red_cases.add((nx,ny))
nx_2 = x_blue + dx[i]
ny_2 = y_blue + dy[i]
if 0 <= nx_2 < n and 0 <= ny_2 < m and maze[nx_2][ny_2] != 5 and (nx_2,ny_2) not in visited[1]:
blue_cases.add((nx_2,ny_2))
return red_cases, blue_cases
def dfs(red,blue,count): # 완전 탐색(DFS) 함수
nonlocal minimum
nonlocal is_success
red_success = (red == red_end)
blue_success = (blue == blue_end)
if red_success and blue_success: # 빨강 파랑 모두 도착했을 경우
minimum = min(minimum, count)
is_success = True
return
if count >= minimum: # 백트래킹(가지치기)
return
red_cases, blue_cases = get_all_cases(red,blue,visited)
if red_success: # 빨강만 도착한 경우
for next_blue in blue_cases:
if next_blue == red:
continue
visited[1].add(next_blue)
dfs(red,next_blue,count+1)
visited[1].remove(next_blue)
elif blue_success: # 파랑만 도착한 경우
for next_red in red_cases:
if next_red == blue:
continue
visited[0].add(next_red)
dfs(next_red,blue,count+1)
visited[0].remove(next_red)
else: # 빨강 파랑 둘다 아직 도착하지 못한 경우
for next_red in red_cases:
for next_blue in blue_cases:
if next_red == next_blue or (next_red == blue and next_blue == red):
continue
visited[0].add(next_red)
visited[1].add(next_blue)
dfs(next_red,next_blue,count+1)
visited[0].remove(next_red)
visited[1].remove(next_blue)
visited = [set([red_start]), set([blue_start])]
dfs(red_start,blue_start,0)
if not is_success:
return 0
else:
return minimum
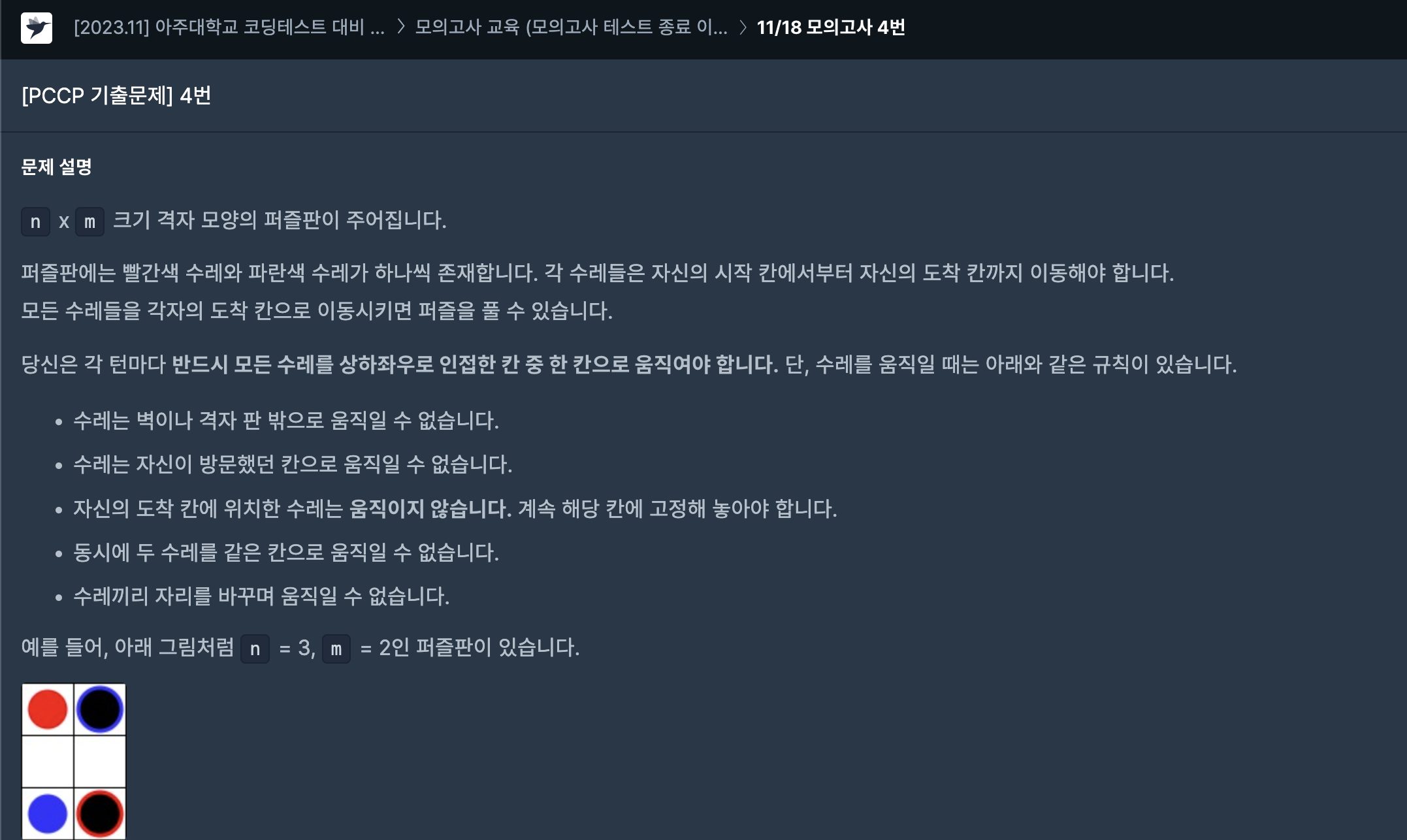
이번 문제는 한 턴마다 파란색 수레와 빨간색 수레를 각각 상하좌우로 움직여야 할 때, 완전 탐색을 통해 파란색 수레와 빨간색 수레가 모두 도착하는 최단 시간을 구하는 문제이다.
오랜만에 완전 탐색 문제를 접해서 그런지 어떻게 모든 경우의 수를 구해야 할지 고민이 되었는데, 강사님의 풀이를 참고해본 결과 빨간색 수레와 파란색 수레가 이동할 수 있는 경우의 수를 구하는 함수를 따로 선언하고, 각 경우의 수마다 2중 for문으로 돌면서 DFS를 재귀 호출하면 된다.
완전 탐색을 위해서는 DFS 함수를 선언하고, 반복문을 사용하여 모든 경우의 수에 DFS 함수를 호출하면 된다. (재귀 탈출을 위한 종료 조건과 visited 원상복구 필수 ⭐️)
다만 수레가 이동할 수 있는 제약조건이 까다로워서 경우의 수를 모두 나눠야 정확하게 풀 수 있다 :)
'Algorithm 💡 > DFS' 카테고리의 다른 글
| [소프티어 6248번] 출퇴근길 (1) | 2024.06.15 |
|---|---|
| [백준 1240번] 노드사이의 거리 (1) | 2024.01.08 |
| [백준 14888번] 연산자 끼워넣기 (0) | 2023.10.06 |
| [프로그래머스 Lv.2] 타겟 넘버 재풀이 (0) | 2023.09.28 |
| [백준 15683번] 감시 (0) | 2023.08.31 |


