

14888번: 연산자 끼워넣기
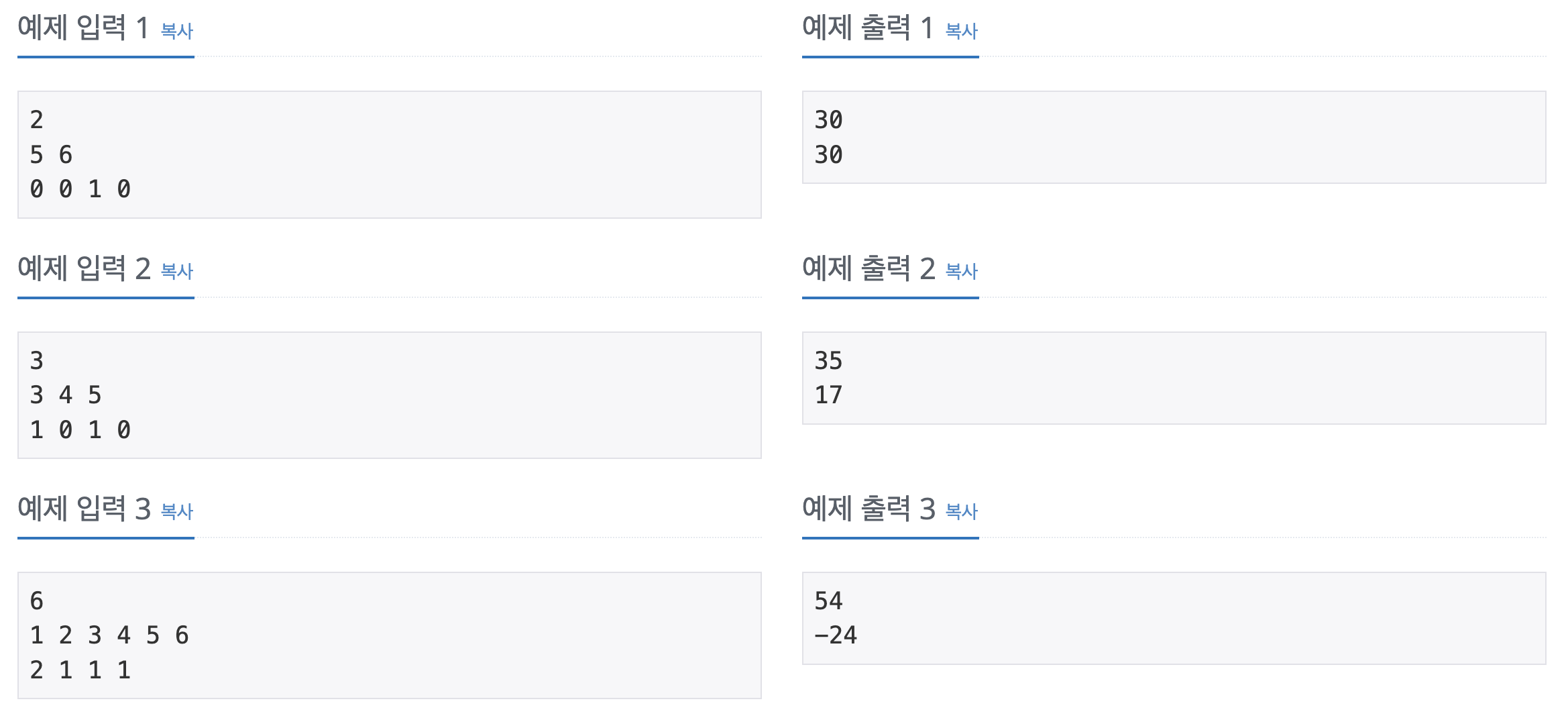
첫째 줄에 수의 개수 N(2 ≤ N ≤ 11)가 주어진다. 둘째 줄에는 A1, A2, ..., AN이 주어진다. (1 ≤ Ai ≤ 100) 셋째 줄에는 합이 N-1인 4개의 정수가 주어지는데, 차례대로 덧셈(+)의 개수, 뺄셈(-)의 개수, 곱
www.acmicpc.net
# 식의 계산은 우선 순위 무시하고 앞에서부터 진행
# 나눗셈은 몫만 취한다(//)
# 음수를 양수로 나눌 때는 음수를 양수로 바꾼 뒤 몫을 취한뒤 음수로 바꾼다
n = int(input())
data = list(map(int,input().split()))
# 0 : 덧셈 개수, 1 : 뺄셈 개수, 2 : 곱셈 개수, 3 : 나눗셈 개수
operator_count = list(map(int,input().split()))
max_value = float("-inf")
min_value = float("inf")
def divide(x,y):
if x < 0 and y > 0:
return -(abs(x)//y)
else:
return x // y
def dfs(index,n):
global max_value
global min_value
if sum(operator_count) == 0: # 모든 연산자를 다 사용한 경우
max_value = max(max_value,n)
min_value = min(min_value,n)
return
if operator_count[0] > 0: # 덧셈
operator_count[0] -= 1
dfs(index+1, n+data[index+1])
operator_count[0] += 1
if operator_count[1] > 0: # 뺄셈
operator_count[1] -= 1
dfs(index+1, n-data[index+1])
operator_count[1] += 1
if operator_count[2] > 0: # 곱셈
operator_count[2] -= 1
dfs(index+1, n*data[index+1])
operator_count[2] += 1
if operator_count[3] > 0: # 나눗셈
operator_count[3] -= 1
dfs(index+1, divide(n,data[index+1]))
operator_count[3] += 1
dfs(0,data[0])
print(max_value)
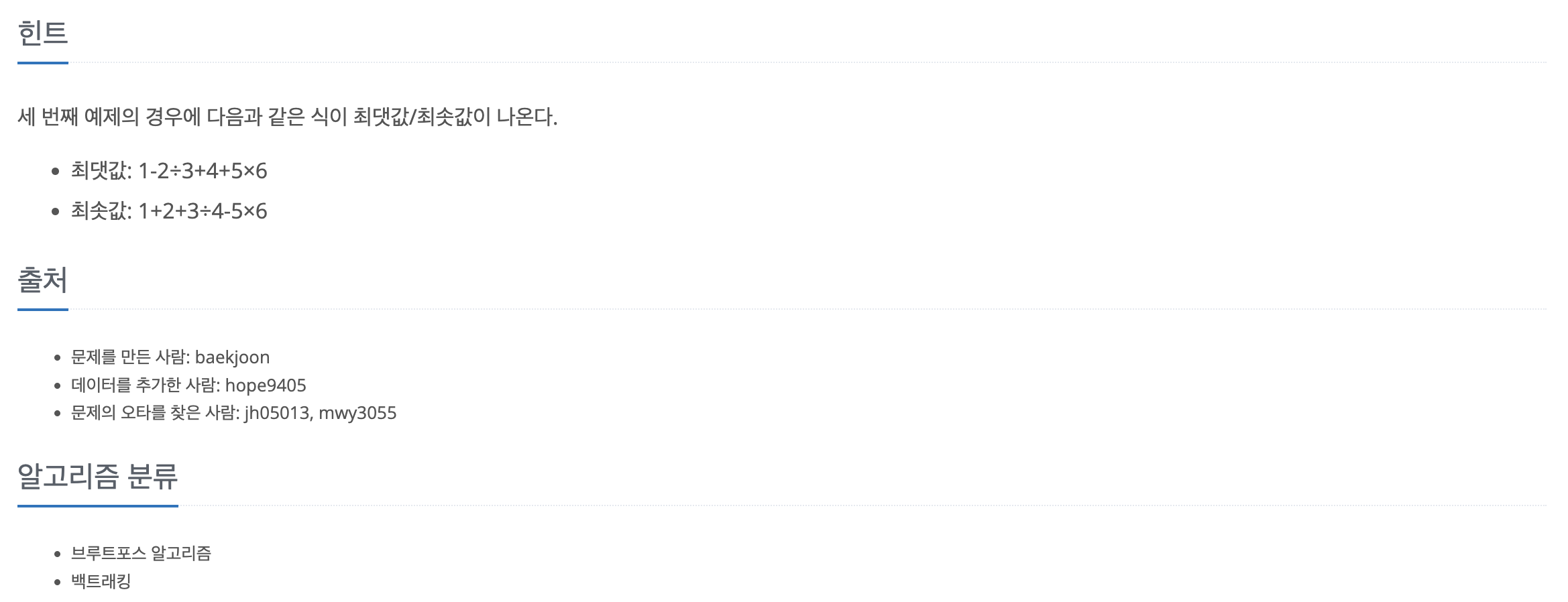
print(min_value)이번 문제는 덧셈 / 뺄셈 / 곱셈 / 나눗셈 4가지 연산의 횟수가 정해져있을 때, 만들 수 있는 식의 결과의 최댓값과 최솟값을 구하는 문제이다.
가장 먼저 최댓값과 최솟값을 float("-inf")와 float("inf")로 초기화하고, 모든 경우의 수를 탐색해보기 위해 DFS 알고리즘을 사용했다.
DFS 알고리즘의 return 조건은 모든 연산자를 사용했을 때(sum(operator_count) == 0)으로 설정하였고, 연산자를 사용할 때 마다 해당 연산의 횟수를 -1 해주고, 해당 경로를 탐색한 후에는 다시 연산 횟수를 +1 해줌으로써 원상복구 시켜주는 방식으로 모든 경우의 수를 탐색했다.
다만 문제에서 주어진 나눗셈 방식을 사용해야 하기 때문에 나눗셈은 별도의 함수로 선언해주어야 했다.
완전탐색을 활용하여 간단하게 풀 수 있었던 문제였다 :)
'Algorithm 💡 > DFS' 카테고리의 다른 글
| [백준 1240번] 노드사이의 거리 (1) | 2024.01.08 |
|---|---|
| [프로그래머스 PCCP 모의고사 2-4번] 수레 (0) | 2023.11.18 |
| [프로그래머스 Lv.2] 타겟 넘버 재풀이 (0) | 2023.09.28 |
| [백준 15683번] 감시 (0) | 2023.08.31 |
| [백준 17070번] 파이프 옮기기1 (1) | 2023.08.28 |


