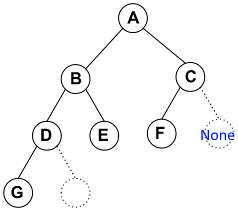
순회하는 것 자체가 재귀이므로, 재귀 함수로 만들면 구현하는 과정을 이해하기 쉽다. 또한 순서만 조금씩 바꾸면 바로 중위 순회와 후위 순회로 변경할 수 있다.
전위 순회 함수 만들기
tree = ["A", "B", "C", "D", "E", "F", None, "G"]
n = len(tree)
def preorder(tree, i):
if i < len(tree):
print(tree[i], end=" ") # 방문 처리(출력)
left, right = 2*i + 1, 2*i + 2
if left < len(tree) and tree[left] is not None:
preorder(tree,left)
if right < len(tree) and tree[right] is not None:
preorder(tree,right)
preorder(tree,0) # A B D G E C F- 방문할 노드의 인덱스가 트리 크기를 넘어가면 종료한다.
- 현재 노드를 방문한다. 방문 처리는 값을 출력하는 것으로 한다.
- 왼쪽 노드의 인덱스와 오른쪽 노드의 인덱스를 구한다.
- 왼쪽 노드의 인덱스가 범위 안에 있고, 해당 노드가 None이 아니면
- 왼쪽 노드를 방문한다. (재귀 호출)
- 오른쪽 노드의 인덱스가 범위 안에 있고, 해당 노드가 None이 아니면
- 오른쪽 노드를 방문한다. (재귀 호출)
중위 순회 함수 만들기
이미 만든 전위 순회 함수의 코드에서 자신을 재귀 호출하는 순서만 바꾸면 된다. 중위 순회는 왼쪽 노드 → 현재(부모) 노드 → 오른쪽 노드 순으로 방문해야 하므로, 아래와 같이 처리한다.
tree = ["A", "B", "C", "D", "E", "F", None, "G"]
n = len(tree)
def inorder(tree, i):
if i < len(tree):
left, right = 2*i + 1, 2*i + 2
if left < len(tree) and tree[left] is not None:
inorder(tree,left)
print(tree[i], end=" ") # 방문 처리(출력)
if right < len(tree) and tree[right] is not None:
inorder(tree,right)
inorder(tree,0) # G D B E A F C
후위 순회 함수 만들기
방문하는 코드의 위치만 바꾼다. 왼쪽 노드 → 오른쪽 노드 방문 → 현재 노드 방문
tree = ["A", "B", "C", "D", "E", "F", None, "G"]
n = len(tree)
def postorder(tree, i):
if i < len(tree):
left, right = 2*i + 1, 2*i + 2
if left < len(tree) and tree[left] is not None:
postorder(tree,left)
if right < len(tree) and tree[right] is not None:
postorder(tree,right)
print(tree[i], end=" ") # 방문 처리(출력)
postorder(tree,0) # G D E B F C A'Data Structure 🛠️ > Tree' 카테고리의 다른 글
| [Tree] Queue를 이용한 레벨 순서 순회 (0) | 2023.09.07 |
|---|---|
| [Tree] 배열로 이진트리 구현하기 (0) | 2023.09.07 |
| [Tree] 트리의 개념 및 이진 트리 순회 (0) | 2023.09.07 |


