트리란 ?
트리(tree)는 그래프(graph)의 한 형태로서, 순환(cycle)이 없는 연결 그래프라 한다.
트리의 구성 요소
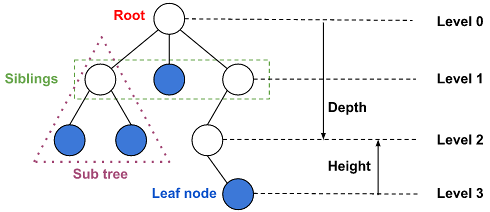
- 노드(Node): 트리를 구성하는 기본 요소, 값(key or data)과 하위 노드를 가리키는 포인터(pointer)를 가진다.
- 간선(Edge): 노드와 노드를 연결한 선 (link)
위 그림처럼 트리는 루트에서 시작한다.
- 루트(Root): 부모 노드가 없는 최상위 노드. 모든 트리의 루트는 하나다.
- 부모(parent) 노드: 자식(child) 노드를 가진 노드
- 자식(child) 노드: 부모 노드의 하위 노드
- 형제(siblings) 노드: 부모가 같은 노드
- 리프(leaf) 노드: 자식이 없는 노드
- 서브 트리(sub tree): 특정 노드를 루트로 생각할 때 생기는 트리
- 크기(size): 자신을 포함한 모든 자식 노드의 개수
- 레벨(level): 루트 노드부터 특정 노드까지 연결된 간선의 수
- 깊이(depth): 루트 노드부터 특정 노드까지의 거리, 수치로만 보면 레벨과 같은 것 같다.
- 높이(height): 노드에서 가장 깊은 노드까지의 길이
- 경로(path): 한 노드에서 다른 노드로 갈 때 거쳐 가는 노드들의 순서
- 차수(degree): 자식의 개수
레벨, 깊이, 높이는 다 비슷해 보인다. 깊이는 루트부터 아래로 내려간 길이이고, 높이는 서브 트리에서 가장 깊은 노드부터 위로 올라간 길이라고 생각하면 될 것 같다.
이진 트리와 순회 방법
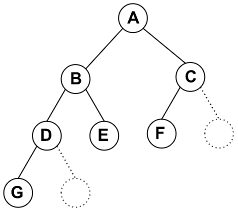
이진트리(binary tree)는 위 그림처럼 모든 노드가 두 개 이하의 자식 노드를 가지는 트리다.
트리에서 각 노드를 한 번씩 체계적으로 방문하는 과정을 순회(traversal)라고 한다.
부모 노드와 왼쪽 노드, 오른쪽 노드를 어떤 순서로 방문하느냐에 따라 순회 방법을 나눈다. 순회 방법에 전위, 중위, 순회, 후위 순회가 있다.
각 노드는 서브 트리일 수 있으므로, 순회하는 방법은 재귀적이다. 위의 세 가지 순회 방법을 재귀적으로 구현하거나 스택을 이용한 구현할 수 있다.
그리고 노드를 레벨 순서로 방문하는 레벨 순서 순회가 있으며, 큐를 이용해서 구현할 수 있다.
1) 전위 순회(Preorder traversal)
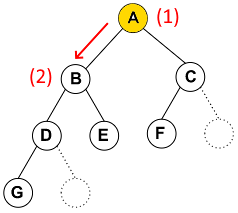
현재 노드를 먼저 방문한다. 그리고 왼쪽 노드와 오른쪽 노드를 차례로 방문한다.
- 먼저 루트인 A부터 방문하고, 왼쪽 B를 방문한다.
- A의 오른쪽인 C를 방문하기 전에, B-D-E가 서브 트리이므로 같은 방법으로 순회한다.
- B는 방문했으므로, B의 왼쪽인 D를 방문한다.
- D도 서브 트리이므로, B의 오른쪽인 E보다 먼저 순회한다.
- D를 이미 방문했으므로, 왼쪽 G를 방문한다.
- B-D-G를 모두 방문했으므로, B의 오른쪽 E를 방문한다.
- A-B-D-G-E를 방문했으므로, A의 오른쪽인 C를 방문한다.
- C의 왼쪽 노드인 F를 방문한다.
2) 중위 순회(Inorder traversal)
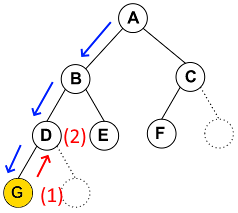
왼쪽 노드를 먼저 방문한 후에 현재 노드를 방문한다. 그리고 오른쪽 노드를 방문한다.
- 먼저 루트 A에서 출발한다. A를 방문하기 전에 왼쪽 B를 먼저 방문해야 한다.
- B-D-E도 서브 트리이므로 B를 방문하기 전에 B의 왼쪽을 먼저 방문해야 한다.
- 이 과정을 반복하면 가장 먼저 방문하는 노드는 G이다.
- D의 왼쪽을 모두 방문했으니, D를 방문하고 D의 오른쪽으로 간다.
- D의 오른쪽은 없으므로, B의 왼쪽인 G-D를 모두 방문했다.
- 그러므로 B를 방문한다. 그리고 B의 오른쪽 노드 E를 방문한다.
- 이렇게 하면 A의 왼쪽인 G-D-B-E를 모두 방문했다.
- 그러므로 A를 방문한다. 이제 A의 오른쪽으로 간다.
- 마찬가지로 C를 방문하기 전에 C의 왼쪽 F를 먼저 방문한다.
- 마지막으로 C를 방문한다.
3) 후위 순회(Postorder traversal)
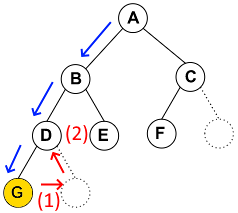
왼쪽 노드를 먼저 방문한다. 그리고 오른쪽 노드와 현재 노드를 차례로 방문한다.
- 먼저 루트 A에서 출발한다. A를 방문하기 전에 왼쪽 B를 먼저 방문해야 한다.
- B-D-E도 트리 구조이므로 B를 방문하기 전에 B의 왼쪽을 먼저 방문해야 한다.
- 이 과정을 반복하면 가장 먼저 방문하는 노드는 G이다.
- D의 왼쪽을 모두 방문했으니, D의 오른쪽으로 간다.
- D의 오른쪽은 없으므로, D의 왼쪽과 오른쪽을 다 방문했다. 이제 D를 방문한다.
- B의 왼쪽인 G-D를 방문했으므로, B의 오른쪽 노드 E를 방문하고 B를 방문한다.
- 이렇게 하면 A의 왼쪽인 G-D-E-B를 모두 방문했다.
- 이제 A의 오른쪽으로 간다.
- 마찬가지로 C를 방문하기 전에 C의 왼쪽 F를 먼저 방문한다.
- C의 오른쪽은 없으니 C를 방문한다.
- 마지막으로 A를 방문한다.
4) 레벨 순서 순회(Level order traversal)
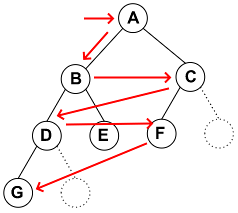
레벨 0부터 차례로 방문하며, 같은 레벨에서는 왼쪽에서 오른쪽으로 가면서 방문한다.
출처 : https://wikidocs.net/193702
07. 파이썬으로 트리 구현하기
트리(tree)는 족보의 가계도나 조직도를 떠올리면 된다. 또는 마인드맵을 생각하자. 어려운 말로는 그래프(graph)의 한 형태로서, 순환(cycle)이 없는 연결 그래프라 한…
wikidocs.net
'Data Structure 🛠️ > Tree' 카테고리의 다른 글
| [Tree] Queue를 이용한 레벨 순서 순회 (0) | 2023.09.07 |
|---|---|
| [Tree] 이진트리 재귀 순회 함수 만들기 (0) | 2023.09.07 |
| [Tree] 배열로 이진트리 구현하기 (0) | 2023.09.07 |


