1) Dynamic Programming 이란 ?
Dynamic Programming은 또 다른 자료구조(메모리)에 계산한 정보들을 저장함으로써 중복되는 연산을 줄이고, 이로써 프로그램의 수행 속도를 개선하는 알고리즘이다.
DP는 완전 탐색(BFS, DFS)과 같이 수많은 경우의 수를 따져보아야 할 때, 경우의 수가 수없이 많을 때 메모리 공간을 사용하여 수행시간을 단축시키는 알고리즘이다.
여러 개의 작은 문제들을 먼저 푼 후에 그 결과를 바탕으로 더 큰 문제를 해결하는 알고리즘으로, 한번 계산한 문제는 다시 계산하지 않도록 메모리에 저장하고, 필요한 경우 다시 계산하지 않고 저장된 값을 사용한다.(매 순간 최적의 값을 저장함)
쉽게 설명하면 문제를 해결하기 위한 점화식을 찾아낸 후 점화식의 항을 밑에서부터 차례로 구해나가면서 답을 구하는 형태의 알고리즘이다.
피보나치 수열의 점화식을 재귀 함수를 사용해 만들 순 있지만, 단순하게 매번 계산하도록 하면 문제를 효율적으로 해결할 수 없다.
이러한 문제는 DP를 사용하면 효율적으로 해결할 수 있다. 단 다음 조건들을 만족할 때 사용할 수 있다.
2) DP를 사용할 수 있는 경우
1. 큰 문제(Problem)를 여러 개의 작은 문제(Sub Problem)들로 나눌 수 있을 때
2. 작은 문제에서 구한 정답들로 그것을 포함하는 더 큰 문제의 정답을 구할 수 있을 때
3. 작은 문제들의 정답들이 중복적으로 연산될 때(Memoization 기법을 통해 필요한 연산의 수를 줄일 수 있음)
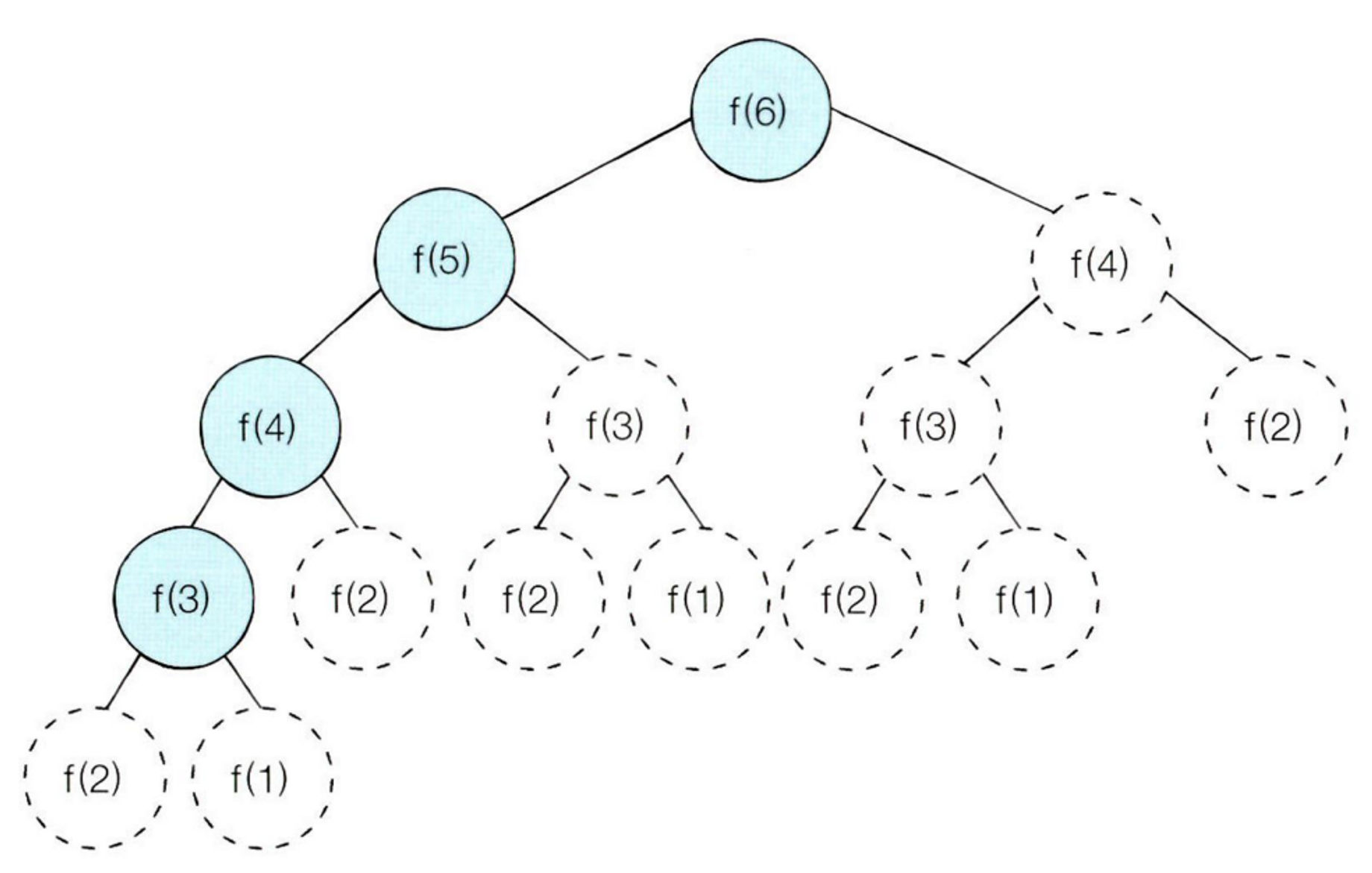
3-1) Top-down 방식
피보나치 수열은 이러한 조건을 만족하는 대표적인 문제이다. 이 문제를 “메모이제이션(Memoization) 기법”을 사용해서 해결해보자.
메모이제이션(캐싱, Caching)은 DP를 구현하는 방법 중 한 종류로, 한 번 구한 결과를 메모리 공간에 메모해두고 같은 식을 다시 호출하면 메모한 결과를 그대로 가져오는 기법이다.
# 한번 계산된 결과를 메모이제이션 하기 위한 리스트 초기화
d = [0] * 100
# 피보나치 함수를 재귀함수로 구현(탑 다운 DP)
def fibo(x):
if x == 1 or x == 2:
return 1
# 이미 계산한 적 있는 값이라면 그대로 반환
if d[x] != 0:
return d[x]
# 아직 계산하지 않은 값이라면 점화식에 따라서 피보나치 결과를 메모리에 저장하고 반환
d[x]=fibo(x-1)+fibo(x-2)
return d[x]
print(fibo(99))⇒ O(N) !!
정리하자면 DP는 큰 문제를 작게 나누고, 같은 문제라면 한 번씩만 풀어 문제를 효율적으로 해결하는 알고리즘 기법이다.(DP와 분할 정복의 차이점은 DP는 문제들이 서로 영향을 미치고 있다는 점이다.)
이처럼 '재귀 함수'를 이용하여 DP 소스코드를 작성하는 방법을 큰 문제를 해결하기 위해 작은 문제를 호출한다고 하여 Top-Down 방식이라고 말한다.
3-2) Bottom-up 방식
# 앞서 계산된 결과를 저장하기 위한 DP 테이블 초기화
d = [0] * 100
# 첫 번째 피보나치 수와 두 번째 피보나치 수 1
d[1] = 1
d[2] = 1
n = 99
# 피보나치 함수를 반복문으로 구현(Bottom-Up DP)
for i in range(3,n+1):
d[i] = d[i-1] + d[i-2]
print(d[n])반면에 단순히 '반복문'을 이용하여 소스코드를 작성하는 경우 작은 문제부터 차근차근 답을 도출한다고 하여 Bottom-Up 방식이라고 말한다.(일반적으로 반복문을 이용한 DP가 더 성능이 좋고 오버헤드가 적다.)
Top-Down 방식은 하향식이라고 하며, Bottom-Up 방식은 상향식이라고 한다.
DP의 전형적인 형태는 Bottom-Up 방식이다. 이 방식에서 사용되는 결과 저장용 리스트는 ‘DP 테이블’이라고 부르며, 메모이제이션은 Top-Down 방식에 국한되어 사용되는 표현이다.
그리고 가능하다면 재귀 함수를 이용하는 Top-Down 방식보다는 Bottom-Up 방식으로 구현하는 것을 권장한다. (왜냐하면 시스템 상 재귀 함수의 스택 크기가 한정되어 있을 수 있기 때문)
⇒ setrecursionlimit() 함수로 재귀 제한 해결가능 !
앞서 수열은 배열이나 리스트로 표현할 수 있다고 했는데, 메모이제이션은 때에 따라서 사전(dict) 자료형을 이용할 수도 있다.
사전 자료형은 수열처럼 연속적이지 않은 경우에 유용한데, an을 계산할 때 a0 ~ an-1 모두가 아닌 일부의 작은 문제에 대한 답만 필요한 경우가 그 예이다.
코딩 테스트에서의 DP 문제는 대체로 간단한 형태로 출제되므로, 이 책에서 다루는 문제 정도만 바르게 습득해도 코딩 테스트에서 DP 문제를 풀기에는 큰 어려움이 없을 것이다.
2) DP 문제의 유형을 파악하는 방법
문제를 푸는 첫 번째 단계는 주어진 문제가 DP 유형임을 파악하는 것이다.
특정한 문제를 완전 탐색 알고리즘으로 접근했을 때 시간이 매우 오래 걸리면 DP를 적용할 수 있는지를 확인하기 위해 해결하고자 하는 부분 문제들의 중복성 여부를 체크하자.
DP는 특정 유형에 국한되지 않고 다양한 유형의 문제를 최적화할 때 고려할 수 있는 알고리즘이다.
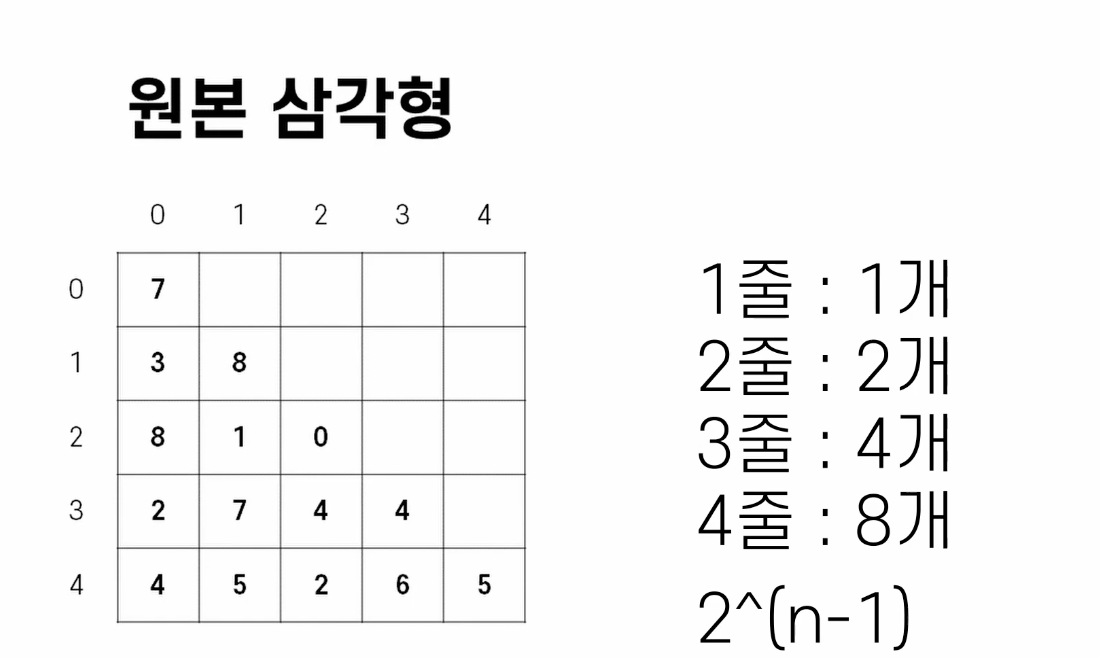
문제를 풀 때 최악의 경우의 수를 계산하는 가장 간단한 방법은 직접 계산해보는 것이다.(패턴이 보일 때까지 경우의 수를 계산)
1. DFS/BFS로 풀 순 있지만 경우의 수가 너무 많은 문제
2. 경우의 수들에 '중복되는 연산'이 많은 경우
3. 작은 문제들부터 계산해서 문제를 해결할 수 있는 경우
DP는 작정하고 어렵게 하고자 한다면 한도 끝도 없이 어려워지지만 코딩테스트에 나올 수준의 DP 문제는 일단 점화식만 찾고나면 그 뒤는 초기 값을 채워넣은 후에 반복문을 돌면서 배열을 채우면 끝이어서 구현이 굉장히 쉽다.
3) DP 문제풀이 방법
- DP 테이블 정의하기(1차원 리스트라면 각 i번째 값이 무엇을 의미하는지, 2차원 리스트라면 가로축과 세로축이 무엇을 의미하는지 이해할 것)
- 점화식(패턴) 찾기
- 초기값 설정하기(점화식이 돌아갈 수 있게 하기 위한 초기값이 어디까지인지를 고민해서 초기값을 설정해야 함)
- 최대한 많은 문제들을 풀어보고 풀이들을 참고하면서 DP식 사고방식을 길러야 함
- 어떻게 하면 반복적인 연산을 줄일 수 있는지, 뒤로 돌아가지 않을 수 있는지, 현재까지 연산을 잘 했다면 이 연산을 어떻게 하면 반복하지 않을 수 있는지, 어떤 방식으로 계산한 정보를 누적해야 할지를 고민해야함
- DP 테이블과 같이 별도의 자료구조를 만들고 이 자료구조에 어떤 정보를 담아야 연산을 반복하지 않을 수 있을지 고민해야함
👉🏻 현재까지의 최적의 해답을 쌓아간다는 방식으로 풀이해야함 ⭐️
DP는 항상 이전에 계산된 값을 활용한다는 점을 명심하자 .. ! ✊🏻
'Algorithm 💡 > DP' 카테고리의 다른 글
| [백준 9461번] 파도반 수열 (0) | 2023.03.02 |
|---|---|
| [백준 1904번] 01타일 (2) | 2023.03.01 |
| [백준 9184번] 신나는 함수 실행 (0) | 2023.03.01 |
| [백준 24416번] 알고리즘 수업 - 피보나치 수 1 (0) | 2023.02.28 |
| [프로그래머스 Lv.3] 정수 삼각형 (0) | 2023.02.28 |



