[SWEA 1949번] 등산로 조성

SW Expert Academy

t = int(input())

dx = [-1,1,0,0]
dy = [0,0,-1,1]

for index in range(t):

    n, k = map(int,input().split())

    area = [list(map(int,input().split())) for _ in range(n)]
    visited = [[False]*n for _ in range(n)]

    maximum_value = max(map(max,area))

    maximum_set = set()

    answer = -1

    for i, row in enumerate(area):
        for j, value in enumerate(row):
            if value == maximum_value:
                maximum_set.add((i,j))

    def dfs(x,y,depth,available):

        global answer

        visited[x][y] = True
        
        for i in range(4):
            nx, ny = x+dx[i], y+dy[i]

            if 0 <= nx < n and 0 <= ny < n and not visited[nx][ny]:
                if area[nx][ny] < area[x][y]:
                    dfs(nx,ny,depth+1,available)
                else:
                    if available and abs(area[nx][ny] - area[x][y]) < k:
                        diff = abs(area[nx][ny] - area[x][y])+1
                        area[nx][ny] -= diff
                        dfs(nx,ny,depth+1, False)
                        area[nx][ny] += diff

        answer = max(answer,depth)

        visited[x][y] = False

    for mx,my in maximum_set:
        dfs(mx,my,1,True)
    
    print(f"#{index+1} {answer}")

 

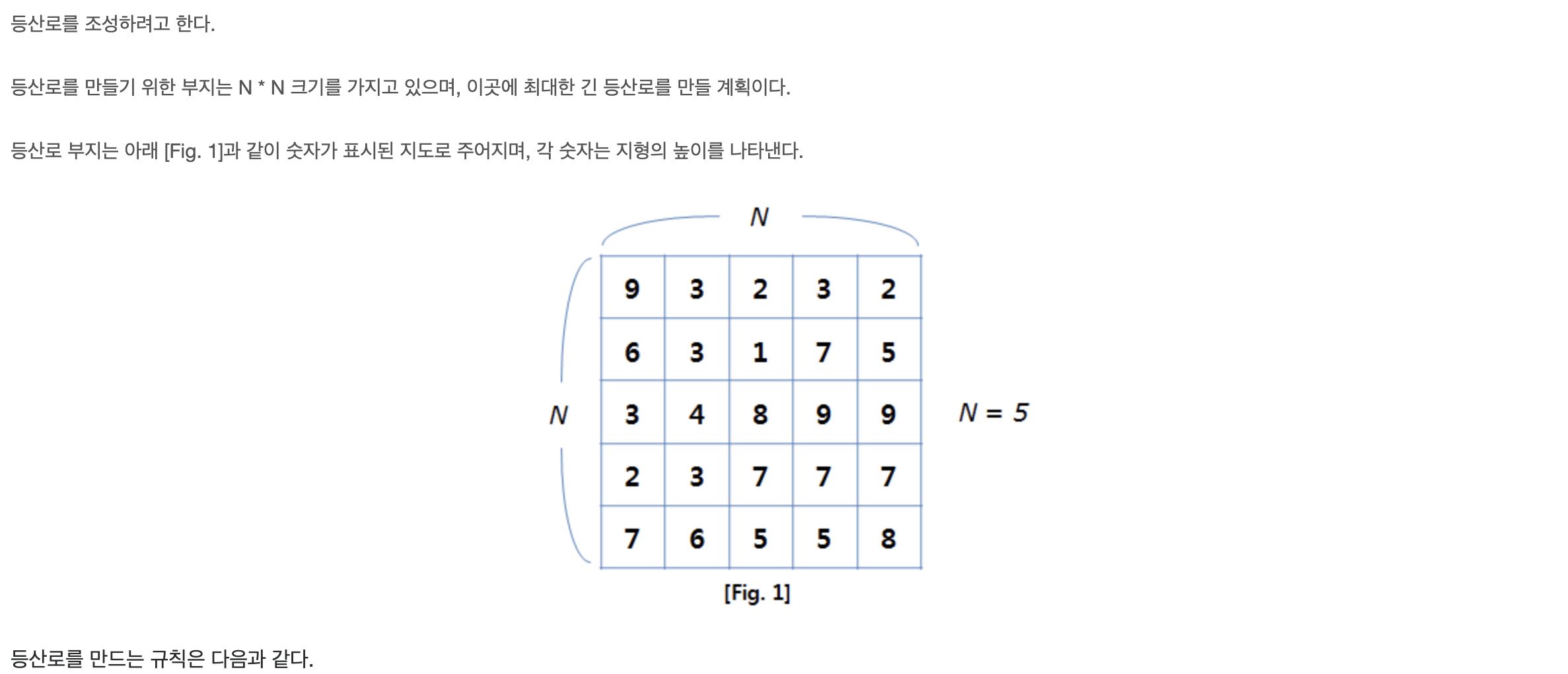
이번 문제는 가장 높은 좌표에서부터 시작하여 가장 길게 만들 수 있는 등산로의 길이를 구하는 문제이다.

 

모든 경우의 수를 탐색하기 위해 DFS 함수를 사용하였고, '긴 등산로를 만들기 위해 딱 한 곳을 정해서 최대 K 깊이만큼 지형을 깎는 공사를 할 수 있다.' 라는 조건 때문에 딱 한 곳만 공사가 가능하기 때문에 공사 여부(available)를 인자로 전달해주었다.

 

전형적인 완전탐색 문제였다 :)