


# 정답 코드(BFS + 최단경로)
from collections import deque
T = int(input())
for test_case in range(1, T + 1):
n = int(input())
dx = [-1,1,0,0]
dy = [0,0,-1,1]
area = [list(map(int,(list(input())))) for _ in range(n)]
visited = [[False]*n for _ in range(n)]
time = [[0]*n for _ in range(n)]
def bfs():
visited[0][0] = True
queue = deque([(0,0)])
while queue:
x, y = queue.popleft()
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if 0 <= nx < n and 0 <= ny < n:
if not visited[nx][ny]: # 방문하지 않은 경우
visited[nx][ny] = True
time[nx][ny] = time[x][y] + area[nx][ny]
queue.append((nx,ny))
else:
if time[nx][ny] > time[x][y] + area[nx][ny]:
time[nx][ny] = time[x][y] + area[nx][ny]
queue.append((nx,ny))
bfs()
print(f"#{test_case} {time[n-1][n-1]}")
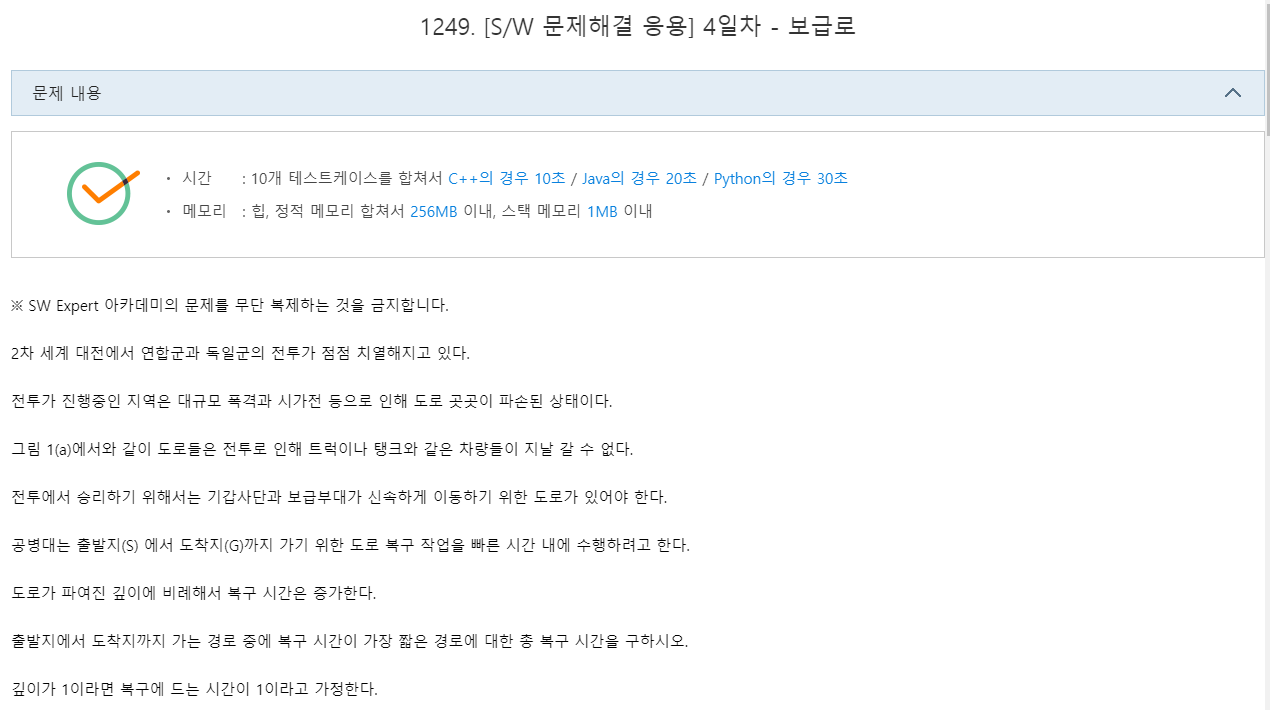
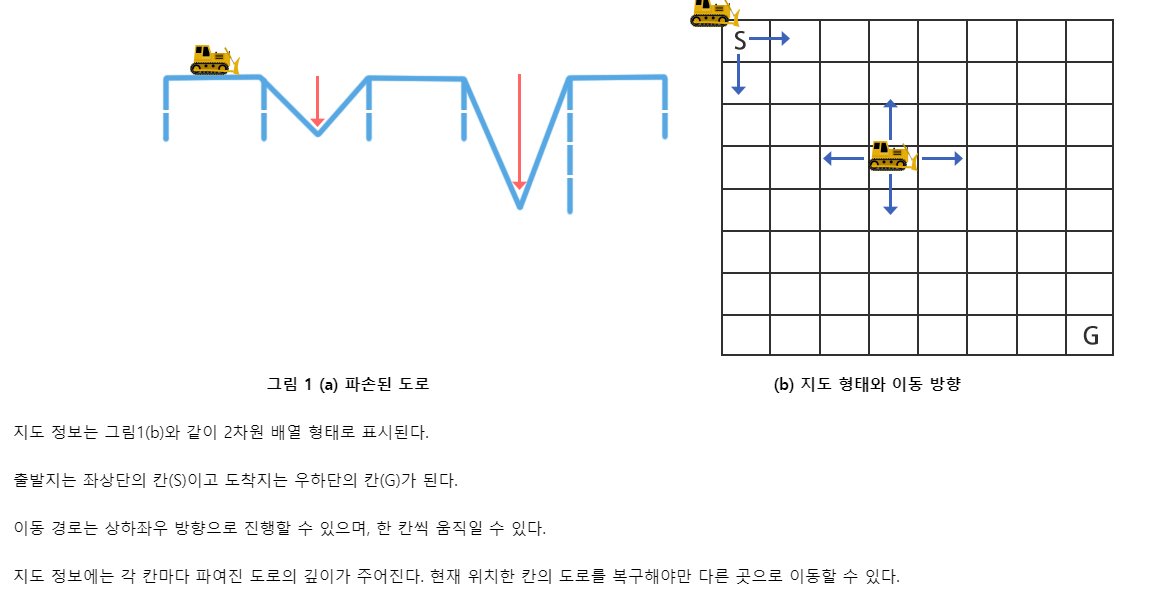
이번 문제는 (0,0) 지점에서 (n-1,n-1) 까지 최소 비용으로 도착했을 때의 비용을 구하는 문제이다.
# 시간초과 코드(DFS + 백트래킹)
from collections import deque
T = int(input())
for test_case in range(1, T + 1):
n = int(input())
INF = float("inf")
dx = [-1,1,0,0]
dy = [0,0,-1,1]
area = [list(map(int,(list(input())))) for _ in range(n)]
visited = [[False]*n for _ in range(n)]
minimum = INF
visited[0][0] = True
def dfs(x,y,total):
global minimum
if x == n-1 and y == n-1:
minimum = min(minimum, total)
return
if total >= minimum: # 백트래킹
return
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if 0 <= nx < n and 0 <= ny < n and not visited[nx][ny]:
visited[nx][ny] = True
dfs(nx,ny,total + area[nx][ny])
visited[nx][ny] = False
dfs(0,0,0)
print(minimum)
처음에는 DFS + 백트래킹 으로 풀이하려고 했었는데, 경우의 수가 너무 많아서 그런지 시간초과가 발생하였다.
따라서 다른 분의 풀이와 Chat GPT를 참고해본 결과, DFS를 사용해서 풀이하게 되면 시간복잡도가 O(4^(N^2))가 된다.
+ 백트래킹으로 효율성을 개선해도 시간초과 발생
주어진 코드는 깊이 우선 탐색(DFS)을 사용하여 좌측 상단 지점에서 우측 하단 지점까지의 최소 합을 찾는 것으로 보입니다. 코드의 시간 복잡도는 DFS의 특성에 따라 결정됩니다.
DFS의 시간 복잡도는 탐색하는 모든 경로의 길이에 비례합니다. 코드에서 각 셀에서는 상하좌우 4개의 이동 방향이 있으므로, 각 셀을 방문할 때마다 4개의 경로가 생성됩니다. 따라서 모든 가능한 경로의 수는 4^(N^2)이 됩니다.
따라서 코드의 시간 복잡도는 O(4^(N^2))입니다. 이는 지수 시간 복잡도로, 입력 크기가 커짐에 따라 매우 빠르게 증가하는 것을 의미합니다. 따라서 이 코드는 큰 입력에 대해서는 비효율적일 수 있습니다. Memoization이나 다이나믹 프로그래밍과 같은 기법을 사용하여 중복 계산을 피하거나 최적화할 수 있습니다.
- Chat GPT
따라서 다익스트라 알고리즘의 아이디어와 비슷하게, BFS로 모든 영역을 한번만 탐색(O(N^2))하면서 이미 방문한 지점이더라도 '현재 까지의 시간 + 비용'이 '이미 방문한 지점'보다 비용이 적다면, 이를 갱신해주는 방식으로 풀이할 수 있다.
주어진 코드는 너비 우선 탐색(BFS)을 사용하여 좌측 상단 지점에서 우측 하단 지점까지의 최소 시간을 계산하는 것으로 보입니다. 코드의 시간 복잡도는 BFS의 특성에 따라 O(V + E)로 표현할 수 있습니다. 여기서 V는 정점(셀)의 수이고, E는 간선(인접한 셀 사이의 이동)의 수입니다.
코드에서 각 정점은 최대 한 번만 방문되기 때문에 V는 N^2에 비례합니다. E는 각 정점에서 상하좌우로 최대 4개의 인접 정점이 있을 수 있으므로, 최악의 경우 E는 4V에 비례합니다.
따라서 코드의 시간 복잡도는 O(V + E) = O(N^2)입니다. 주어진 코드는 효율적으로 동작하며, 크기가 큰 입력에 대해서도 비교적 빠르게 결과를 반환할 것으로 기대됩니다.
- Chat GPT
처음에는 간단한 문제인줄 알았는데, N의 크기가 최대 100 이므로 완탐 + 백트래킹으로 풀이하더라도 시간초과가 발생할 수 밖에 없다.
BFS를 활용한 최단 경로를 풀어볼 수 있었던 좋은 문제였다 :)
SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com
'Algorithm 💡 > BFS' 카테고리의 다른 글
| [백준 11123번] 양 한마리... 양 두마리... (1) | 2024.01.06 |
|---|---|
| [백준 5427번] 불 (0) | 2023.12.29 |
| [프로그래머스 PCCP 모의고사 2-2번] 시추관 (0) | 2023.11.18 |
| [프로그래머스 PCCP 모의고사 4번] 보물 지도 (0) | 2023.11.11 |
| [백준 2589번] 보물섬 (0) | 2023.10.20 |



