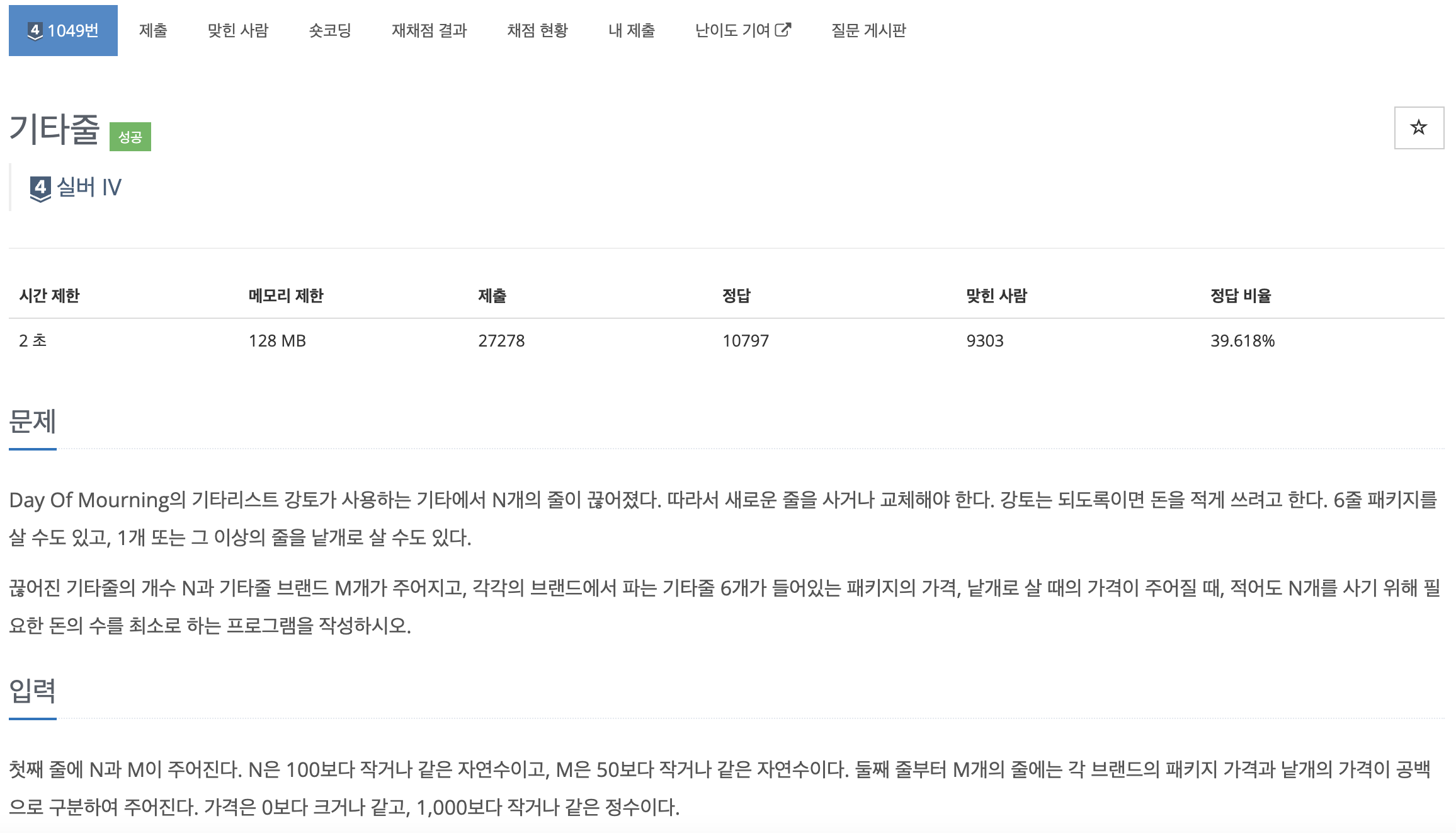
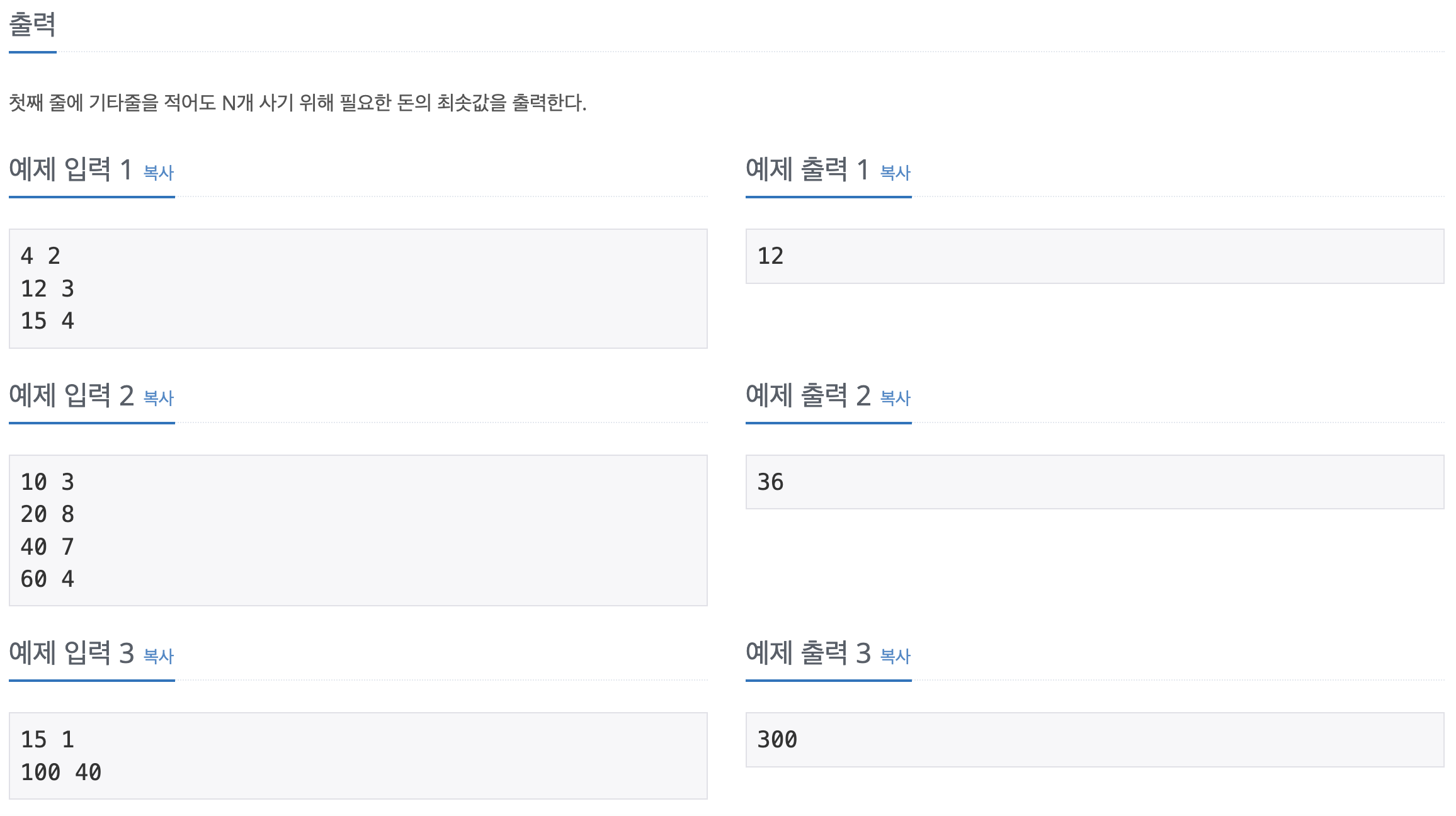

1049번: 기타줄
첫째 줄에 N과 M이 주어진다. N은 100보다 작거나 같은 자연수이고, M은 50보다 작거나 같은 자연수이다. 둘째 줄부터 M개의 줄에는 각 브랜드의 패키지 가격과 낱개의 가격이 공백으로 구분하여 주
www.acmicpc.net
# 끊어진 기타줄 개수 N
# 기타줄 브랜드 M
# 각 브랜드마다 판매중인 6개의 패키지의 가격, 낱개 가격
# 적어도 N개를 사기 위해 필요한 돈의 "최솟값"
n,m = map(int,input().split())
prices = [list(map(int,input().split())) for _ in range(m)]
min_package = min([x[0] for x in prices])
min_item = min([x[1] for x in prices])
if min_package/6 > min_item:
print(min_item*n)
else:
package_count = n // 6
remain_item = n % 6
answer = package_count * min_package + min(min_package,remain_item*min_item)
print(answer)이번 문제는 각 기타줄 브랜드마다 '6개의 줄로 이루어진 패키지 가격'과 '1개로 이루어진 낱개 가격'이 주어졌을 때, N개를 사기 위해서 필요한 최소 비용을 구하는 문제이다.
처음에는 이 문제를 어떻게 풀까 고민을 했었는데, 주어진 테스트 케이스를 하나씩 적어보면서 '어차피 브랜드와 상관없이 개수만 채우면 된다면 패키지 가격이랑 낱개 가격이 가장 가격이 싼 걸 선택하면 되지 않나?' 라는 아이디어를 떠올리게 되었다.
그리고, 패키지로 살지 낱개로만 살지 결정하기 위해서는 (패키지 가격 / 6)이 낱개 가격보다 높은 경우에는 패키지를 살 이유가 없기 때문에 가장 가격이 싼 브랜드의 낱개로만 구매하면 된다.
즉, Greedy 알고리즘을 사용하여 패키지 or 낱개의 가격이 가장 싼 것을 선택하고, 그 패키지의 가격에 따라 사용유무를 결정하게 되면 최소 비용이 나오게 된다 :)
'Algorithm 💡 > Greedy' 카테고리의 다른 글
| [소프티어 6279번] 스마트 물류 (0) | 2024.06.25 |
|---|---|
| [백준 11501번] 주식 (1) | 2023.12.28 |
| [백준 23889번] 돌 굴러가유 (0) | 2023.09.30 |
| [프로그래머스 Lv.1] 체육복 (0) | 2023.09.29 |
| [백준 17392번] 우울한 방학 (0) | 2023.09.29 |



