1) 그래프의 정의

위 그림처럼 도시와 도시 사이를 연결하는 도로나 컴퓨터 네트워크 또는 사람의 인맥 관계처럼 어떤 관계(relationships)를 표현하는 수학 구조를 그래프라고 한다.
도시, 컴퓨터, 사람 등을 노드(node 또는 vertex)라 하고, 이들을 연결하는 도로, 네트워크, 인맥 등을 간선(edges)이라 한다. (많은 자료에서 노드 대신 정점(vertex)이라는 용어를 사용한다.)
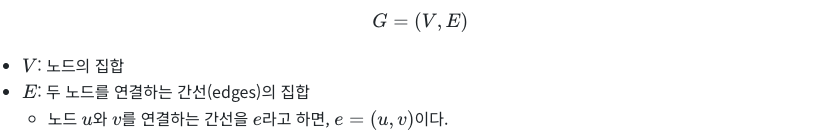
그래프는 '노드의 집합'과 '간선의 집합'으로 구성된다. 이것을 수학으로 표현하면 위와 같다.
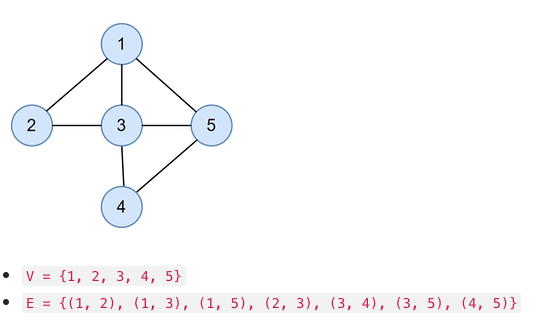
예를 들어 아래 그림과 같은 그래프를 G=(V,E)라고 하면, V와 E는 위와 같다.
2) 그래프의 종류
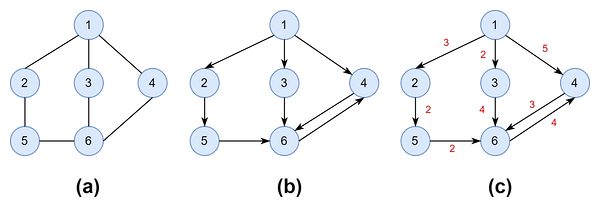
그래프의 종류가 매우 많지만, 우리는 간단하게 세 종류만 공부한다. 그리고, 어떤 노드가 다시 자신과 연결되는 self-loop가 없고, 모두 무방향이거나, 모두 방향인 경우만 다룬다.
2.1) 무방향 그래프(undirected graph)
위 그림의 (a)처럼 두 노드를 연결하는 간선에 방향이 없는 그래프다.
2.2) 방향 그래프(directed graph)
그림 (b)처럼 간선에 방향이 있는 그래프다. 일방통행 도로로 생각하자.
2.3) 가중 그래프(weighted graph)
그림 (c)처럼 노드를 연결하는 간선에 "가중치(weight)"를 부여한 그래프다. 이때 그래프는 무방향 그래프일 수도 있고, 방향 그래프일 수도 있다.
가중치는 한 지점에서 다른 지점으로 이동하는 데 필요한 비용이나 걸리는 시간 등으로 이해하자.
3) Python 으로 Graph 구현하기
프로그래밍에서 그래프를 나타내는 방법은 '인접 행렬' 방식과 '인접 리스트' 방식으로 나눌 수 있다.
- 인접 행렬(Adjacency Matrix) : 2차원 배열로 그래프의 연결 관계를 표현하는 방식
- 인접 리스트(Adjacency List) : 리스트로 그래프의 연결 관계를 표현하는 방식
3.1) 인접 행렬 방식
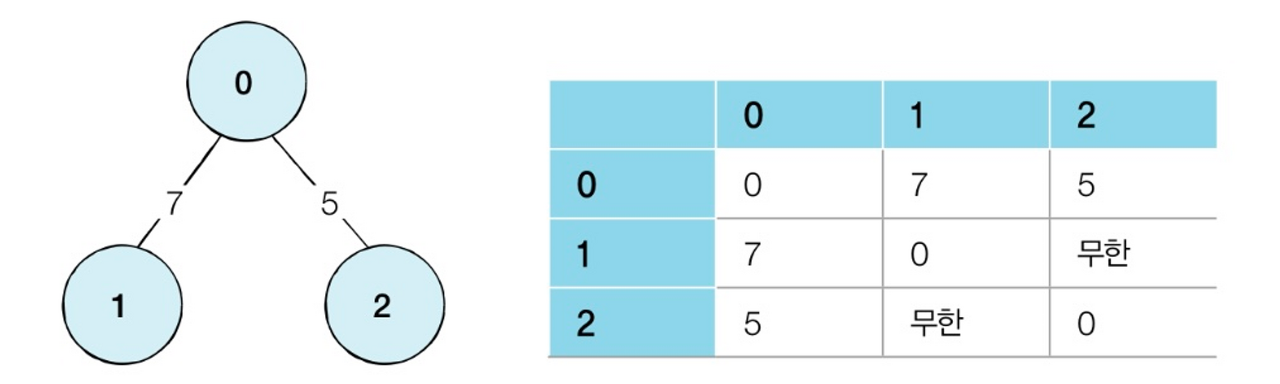
먼저 인접 행렬방식은 2차원 배열에 각 노드가 연결된 형태를 기록하는 방식이다.
INF = 999999999 # 무한의 비용 선언
# 2차원 리스트를 이용하여 인접 행렬 표현
graph = [
[0,7,5],
[7,0,INF],
[5,INF,0]
]
print(graph) # [[0,7,5],[7,0,999999999],[5,999999999,0]]연결이 되어 있지 않은 노드 끼리는 inf(무한)의 비용이라고 작성하고, 실제 코드에서는 논리적으로 정답이 될 수 없는 큰 값 중에서 999999999 등의 값으로 초기화하는 경우가 많다.
3.2) 인접 리스트 방식
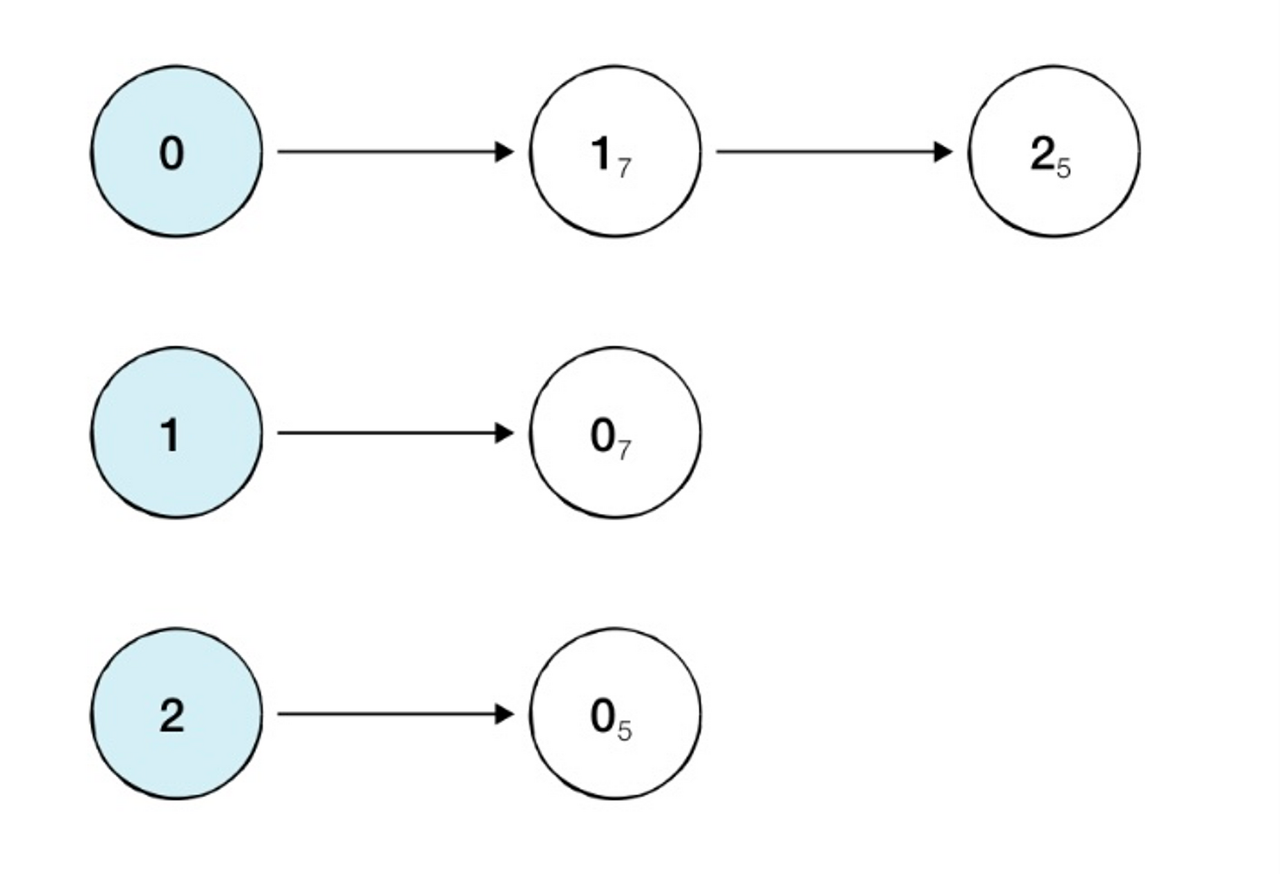
인접 리스트 방식에서는 모든 노드에 연결된 노드에 대한 정보를 차례대로 연결하여 저장한다.
# 행이 3개인 2차원 리스트로 인접 리스트 표현
graph = [[] for _ in range(3)]
# 노드 0에 연결된 노드 정보 저장(노드, 거리)
graph[0].append((1,7))
graph[0].append((2,5))
# 노드 1에 연결된 노드 정보 저장(노드, 거리)
graph[1].append((0,7))
# 노드 2에 연결된 노드 정보 저장(노드, 거리)
graph[2].append((0,5))
print(graph) # [[(1,7),(2,5)],[(0,7)],[(0,5)]]파이썬은 기본 자료형인 리스트 자료형이 append()와 메소드를 제공하므로, 전통적인 프로그래밍 언어에서 배열과 연결 리스트의 기능을 모두 기본으로 제공한다. (파이썬으로 연결 리스트를 이용하여 그래프를 표현하고자 할 때도 2차원 리스트를 이용하면 된다는 점을 기억 !)
3.3) 인접 행렬 방식 vs 인접 리스트 방식
두 방식은 어떤 차이가 있을까 ?
코딩 테스트를 위해 메모리와 속도 측면에서 살펴보자. 메모리 측면에서 보자면 인접 행렬 방식은 모든 관계를 저장하므로 노드의 개수가 많을수록 메모리가 불필요하게 낭비된다.
반면에 인접 리스트 방식은 연결된 정보만을 저장하기 때문에 메모리를 효율적으로 사용한다.
하지만 이러한 속성 때문에 인접 리스트 방식은 인접 행렬 방식에 비해 특정한 두 노드가 연결되어 있는지에 대한 정보를 확인하는 속도가 느리다.
⇒ 인접 리스트 방식에서는 연결된 데이터를 하나씩 확인해야 하기 때문 !
'Data Structure 🛠️ > Graph' 카테고리의 다른 글
| [백준 1238번] 파티 (0) | 2024.07.16 |
|---|---|
| [소프티어 6289번] 우물 안 개구리 (0) | 2024.06.19 |
| [프로그래머스 Lv.3] 가장 먼 노드 (0) | 2023.09.28 |


