25421번: 조건에 맞는 정수의 개수
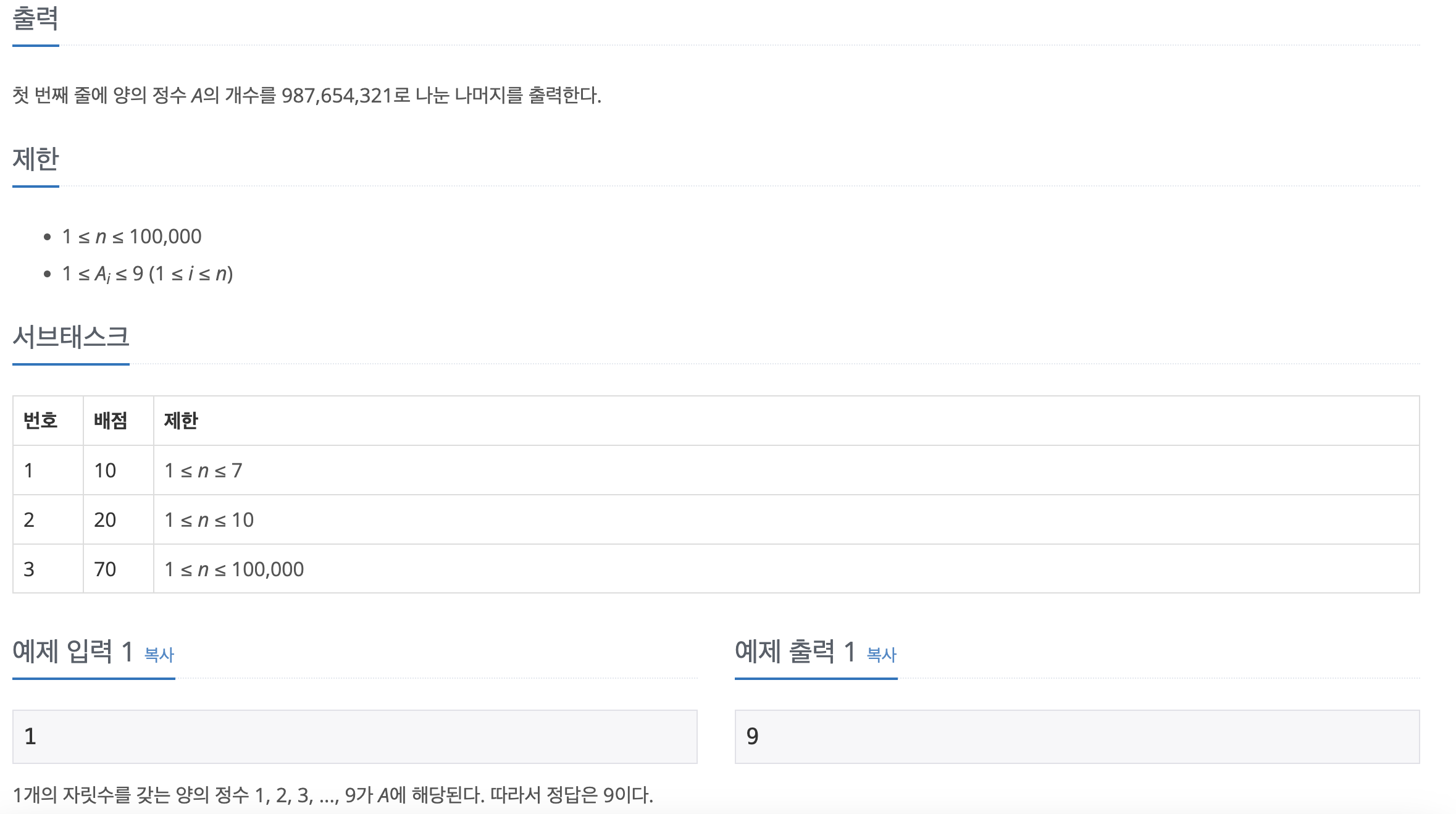
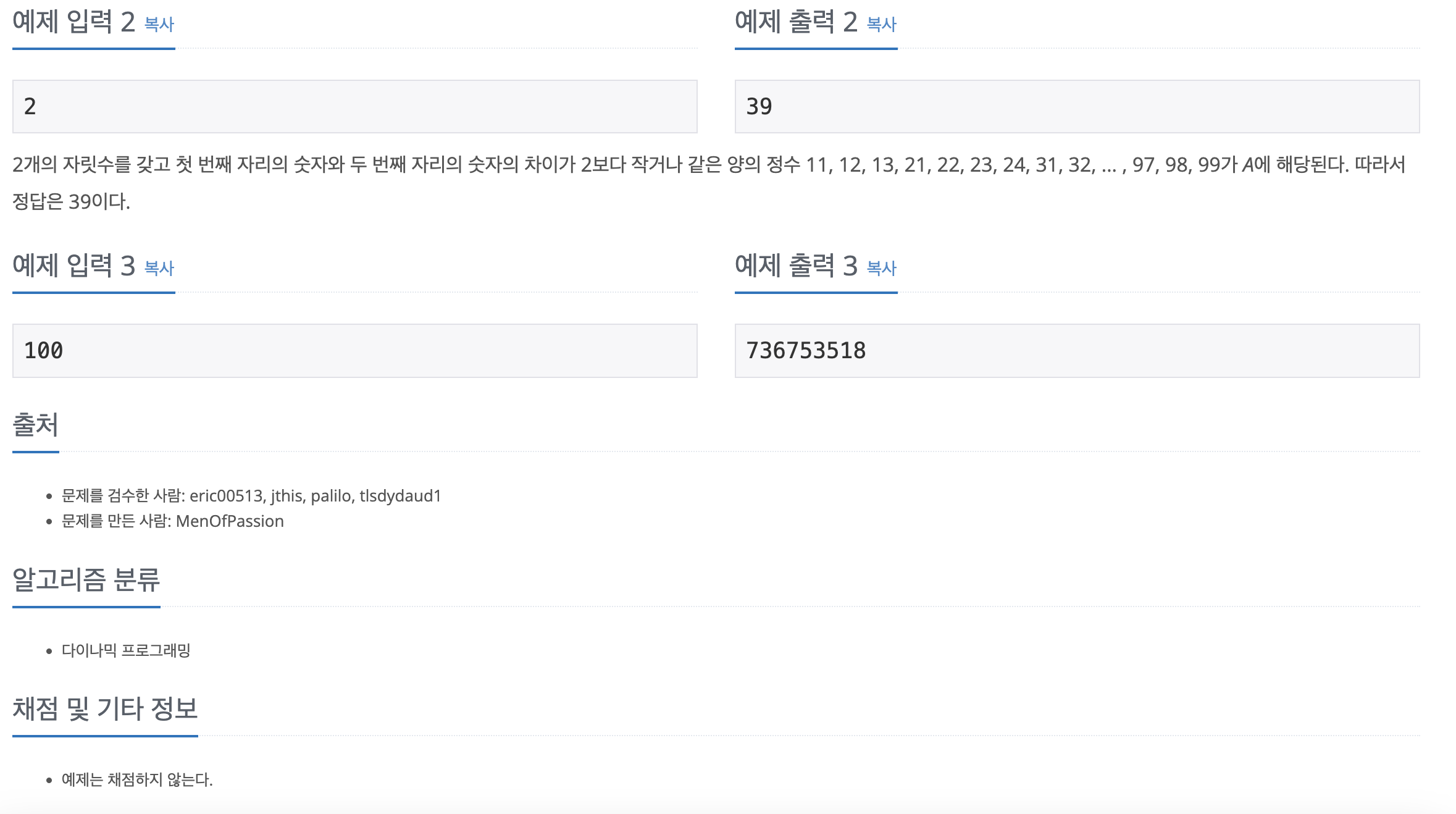
2개의 자릿수를 갖고 첫 번째 자리의 숫자와 두 번째 자리의 숫자의 차이가 2보다 작거나 같은 양의 정수 11, 12, 13, 21, 22, 23, 24, 31, 32, ... , 97, 98, 99가 A에 해당된다. 따라서 정답은 39이다.
www.acmicpc.net
n = int(input())
data = [1 for x in range(1,10)]
for i in range(n-1):
temp = []
for j in range(9):
value = 0
for k in range(j-2,j+3):
if 0 <= k <= 8:
value += data[k]
temp.append(value%987654321)
data = temp
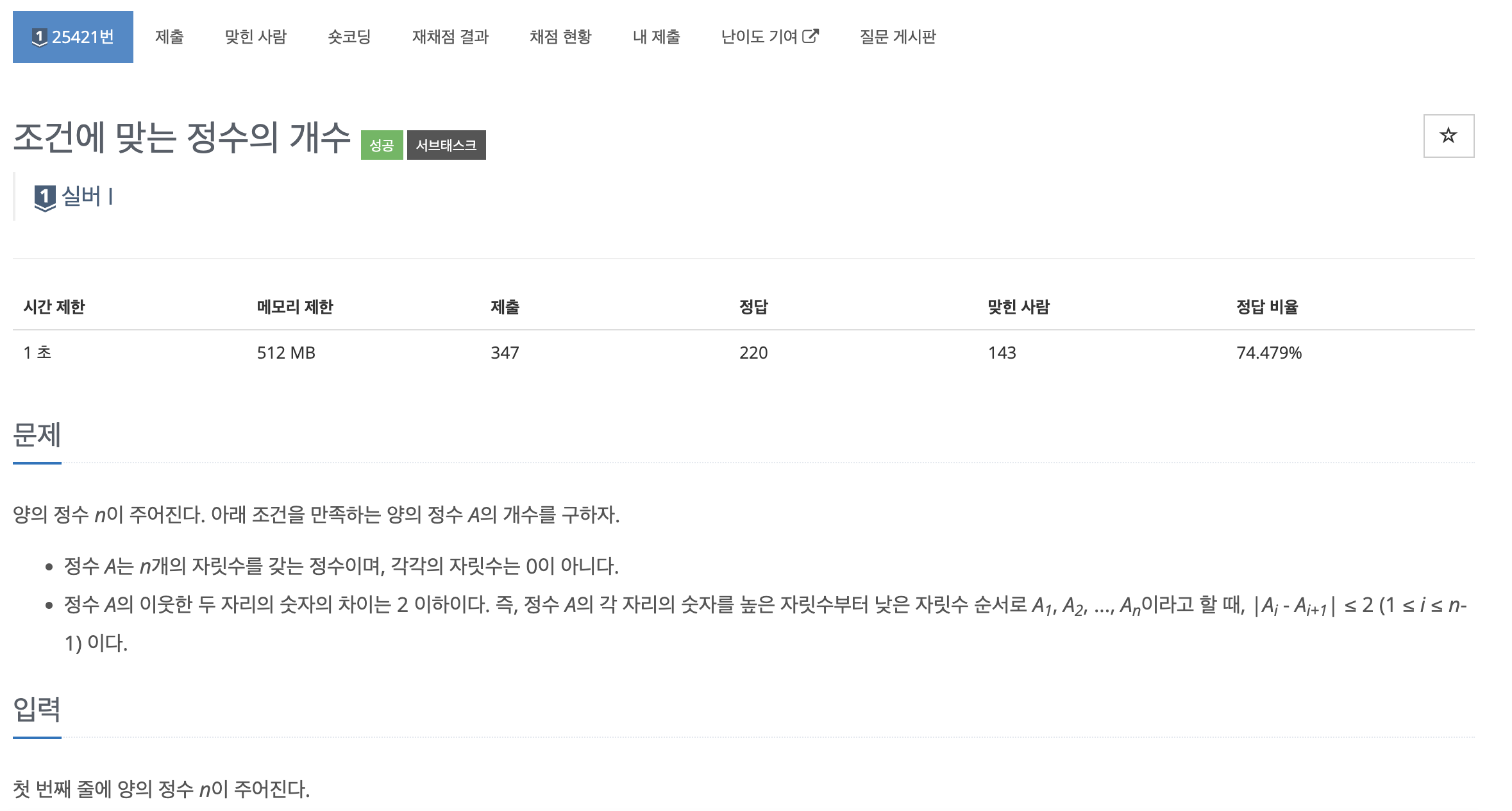
print(sum(data)%987654321)이번 문제는 n개의 0이 아닌 자릿수를 가진 정수 중에서, |Ai - Ai+1| ≤ 2 (1 ≤ i ≤ n-1) 를 만족하는 정수의 개수를 구하는 문제이다.
# DFS를 사용한 30점(시간초과) 코드
def dfs(arr):
global answer
if len(arr) == n:
answer += 1
return
last = arr[-1]
for i in range(last-2,last+3):
if 1 <= i <= 9:
dfs(arr+[i])처음에 문제를 접근할 때는 DFS 알고리즘을 사용하여 완전 탐색으로 풀이했는데, 시간초과가 발생하여 제한시간 내에 풀이할 수 없었다.
따라서 시간복잡도를 줄일 수 있는 방법을 고민하던 중, 결국 현재 자리수는 이전 자리수들에 영향을 받게 된다는 것을 알게 되었고, DP 알고리즘을 바로 떠올릴 수 있었다.
DP를 사용할 수 있는 문제의 조건은 다음과 같다.
1. 큰 문제(Problem)를 작은 문제(Sub Problem)로 나눌 수 있을 때
2. 작은 문제에서 구한 정답들로 그것을 포함하는 더 큰 문제의 정답을 구할 수 있을 때
3. 작은 문제들의 정답들이 중복적으로 연산될 때(Memoization 기법을 통해 필요한 연산의 수를 줄일 수 있음)
따라서 1부터 9까지 자리수를 모두 1로 DP 테이블을 초기화하고, 각 n번동안 자리수를 늘려갈 때마다 (현재 자리수-2, 현재 자리수+2) 범위에 있는 값들을 현재 까지의 개수가 담긴 DP 테이블에 "누적"시켜주었다.
🚨 수정 ) dfs로 푼 코드와 dp로 푼 코드를 둘다 확인해본 결과, 모두 시간복잡도 O(n)로 동일합니다. 따라서 dfs나 dp 중 하나를 선택해서 푸셔도 무관합니다. 하지만 둘다 사용했는데 통과가 되지 않는다면 다음 내용을 확인해보시는 것을 추천드립니다.

하지만 여기서 한 가지 더 조심해야할 점이 있는데, 바로 '모듈러(%987654321)'이다. 중간 과정에서 모듈로 연산을 적용함으로써, 계산 결과를 모듈로 값으로 유지하고 정수 오버플로우를 방지해야 올바른 결과를 얻을 수 있다. (실제로 이것 때문에 30분동안 고생함) ⭐️
그리고 중간 결과에서 모듈로를 적용하더라도 연산 과정에서 오차가 누적될 수 있기 때문에, 최종 결과를 다시 한 번 모듈로 값으로 나누어야 정확한 결과를 얻을 수 있다.
배운 점 및 느낀 점
- 문제를 풀이하기 전에 시간복잡도를 미리 계산하고 어떤 방식으로 풀이할지 고민하는 것이 더 효율적이다.
- 완전 탐색으로 풀이했는데 시간초과가 발생한다면 DP나 백트래킹을 사용할 수 있는 아이디어를 떠올리자.
- 모듈러가 필요한 문제는 중간 과정에서 모듈러 처리를 해주고, 마지막에도 한번 더 해주자. ⭐️