
14500번: 테트로미노
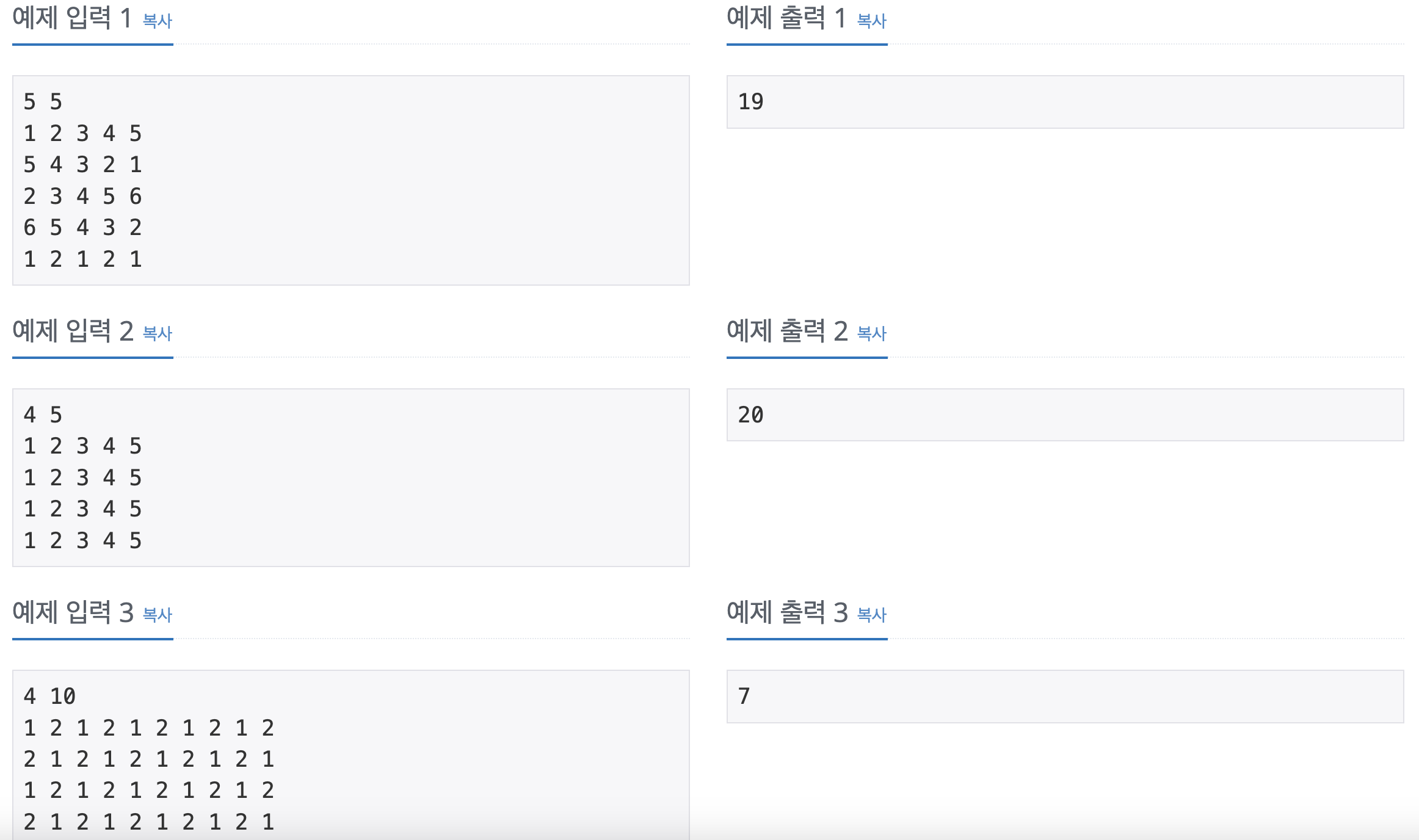
폴리오미노란 크기가 1×1인 정사각형을 여러 개 이어서 붙인 도형이며, 다음과 같은 조건을 만족해야 한다. 정사각형은 서로 겹치면 안 된다. 도형은 모두 연결되어 있어야 한다. 정사각형의 변
www.acmicpc.net
n, m = map(int,input().split())
area = [list(map(int,input().split())) for _ in range(n)]
visited = [[False]*m for _ in range(n)]
dx = [-1,1,0,0]
dy = [0,0,-1,1]
answer = -1
max_value = max(map(max,area))
def dfs(x,y,movement,value):
global answer
# 가지치기(나머지 값들이 모두 최대값이어도 최대값보다 작다면 애초에 계산 X
if answer >= value + area[x][y] + max_value*(4-movement):
return
if movement == 4:
answer = max(answer,value+area[x][y])
return
for i in range(4):
nx, ny = x + dx[i], y + dy[i]
if 0 <= nx < n and 0 <= ny < m and not visited[nx][ny]:
visited[x][y] = True
dfs(nx,ny,movement+1,value + area[x][y])
visited[x][y] = False
def other(x,y):
global answer
if 0 <= x-1 < n and 0 <= x+1 < n and 0 <= y+1 < m:
answer = max(answer, area[x-1][y]+area[x][y]+area[x+1][y]+area[x][y+1])
if 0 <= x+1 < n and 0 <= y-1 < m and 0 <= y+1 < m:
answer = max(answer, area[x][y-1]+area[x][y]+area[x][y+1]+area[x+1][y])
if 0 <= x-1 < n and 0 <= y-1 < m and 0 <= y+1 < m:
answer = max(answer, area[x][y-1]+area[x][y]+area[x][y+1]+area[x-1][y])
if 0 <= x-1 < n and 0 <= x+1 < n and 0 <= y-1 < m:
answer = max(answer, area[x-1][y]+area[x][y]+area[x+1][y]+area[x][y-1])
for i in range(n):
for j in range(m):
dfs(i,j,1,0)
other(i,j)
print(answer)이번 문제는 네 개의 칸으로 이루어진 5가지 모양으로 영역을 선택할 수 있다고 할 때, 해당 영역의 합의 최대 값을 구하는 문제이다.
처음에 문제를 접근했을 땐 모양을 대칭이나 회전 등으로 나올 수 있는 모든 경우의 수를 일일이 다 구해보려고 했는데, 코드를 작성하다보니 이건 아니다라는 생각이 들어 다른 분의 아이디어를 참고하였다.(무엇보다 체크해주어야 하는 경우가 너무 많고 복잡했다.)
놀랍게도 DFS를 사용하면 위와 같은 복잡한 아이디어를 쉽고 간단하게 작성할 수 있었다.
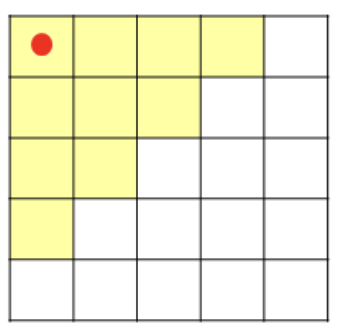
- 테트로미노 중 'ㅗ' 모양 테트로미노를 제외한 나머지 모양들은 DFS를 통해 구할 수 있다. 🌟
- 예시로 빨간 점에서 DFS를 수행한다면 나머지 모양들은 방향과 상관없이 만들 수 있다.
- DFS로 구할 수 없는 'ㅗ' 모양 테트로미노는 따로 처리해준다.(other)


그리고 한가지 중요한 점은, 가지치기로 최적화하지 않고도 문제가 풀리긴 하지만, 가지치기를 사용하면 훨씬 더 빠르게 문제 풀이를 할 수 있다.
배운 점 및 느낀 점
- 경우의 수를 따져보기 힘든 상황에서는 DFS/BFS 알고리즘을 사용할 수 있는지 떠올려보자.
- DFS를 응용하면 여러가지 모양으로 탐색하도록 만들 수 있다.
- 해를 찾아가는 도중, 지금의 경로가 해가 될 것 같지 않으면 그 경로를 더이상 가지 않고 되돌아가는 '가지치기' 기법을 사용하면 시간복잡도를 폭발적으로 줄일 수 있다. (완전 탐색을 하다가 시간 초과가 발생한다면 불필요한 연산을 사전에 차단할 수 있는 조건이 있는지 확인해보자 ✨)
- 현재 상태에서 만들 수 있는 최대값을 이용해서 최대값을 구할 때도 가지치기를 할 수 있다.
'Algorithm 💡 > DFS' 카테고리의 다른 글
| [백준 15683번] 감시 (0) | 2023.08.31 |
|---|---|
| [백준 17070번] 파이프 옮기기1 (1) | 2023.08.28 |
| [백준 9207번] 페그 솔리테어 (0) | 2023.08.23 |
| [백준 15684번] 사다리 조작 (0) | 2023.08.21 |
| [백준 16724번] 피리 부는 사나이 (0) | 2023.08.20 |



