
n,m = map(int,input().split())
area = [list(map(int,input().split())) for _ in range(n)]
move_list = [] # 이동 정보 목록
for i in range(m):
move_list.append(tuple(map(int,input().split())))
cloud_list= {(n-1,0), (n-1,1), (n-2,0), (n-2,1)} # 초기 구름 위치
dx = [0,-1, -1, -1, 0, 1, 1, 1] # 방향 x좌표
dy = [-1, -1, 0, 1, 1, 1, 0, -1] # 방향 y좌표
dx_2 = [-1,-1,1,1] # 대각선 이동을 위한 x좌표
dy_2 = [-1,1,-1,1] # 대각선 이동을 위한 y좌표
total = 0
def move(d,s): # 구름 이동 및 비 내리는 함수
global cloud_list
temp_list = set()
for x,y in cloud_list:
temp_x, temp_y = x+dx[d-1]*s, y+dy[d-1]*s
temp_x = (temp_x % n + n) % n
temp_y = (temp_y % n + n) % n
area[temp_x][temp_y] += 1
temp_list.add((temp_x, temp_y))
cloud_list = temp_list
def waterCopy(): # 물 복사 버그 함수
global cloud_list
for x,y in cloud_list:
for i in range(4):
nx = x + dx_2[i]
ny = y + dy_2[i]
if 0 <= nx < n and 0 <= ny < n and area[nx][ny] > 0:
area[x][y] += 1
def createNewCloud(): # 새로운 구름 생성 함수
global cloud_list
temp = set()
for i in range(n):
for j in range(n):
if area[i][j] >= 2 and (i,j) not in cloud_list: # 문제 해결 코드(집합 자료형으로 in 연산 최적화)
temp.add((i,j))
area[i][j] -= 2
cloud_list = temp
for temp_d,temp_s in move_list:
move(temp_d,temp_s)
waterCopy()
createNewCloud()
for i in range(n):
for j in range(n):
total += area[i][j]
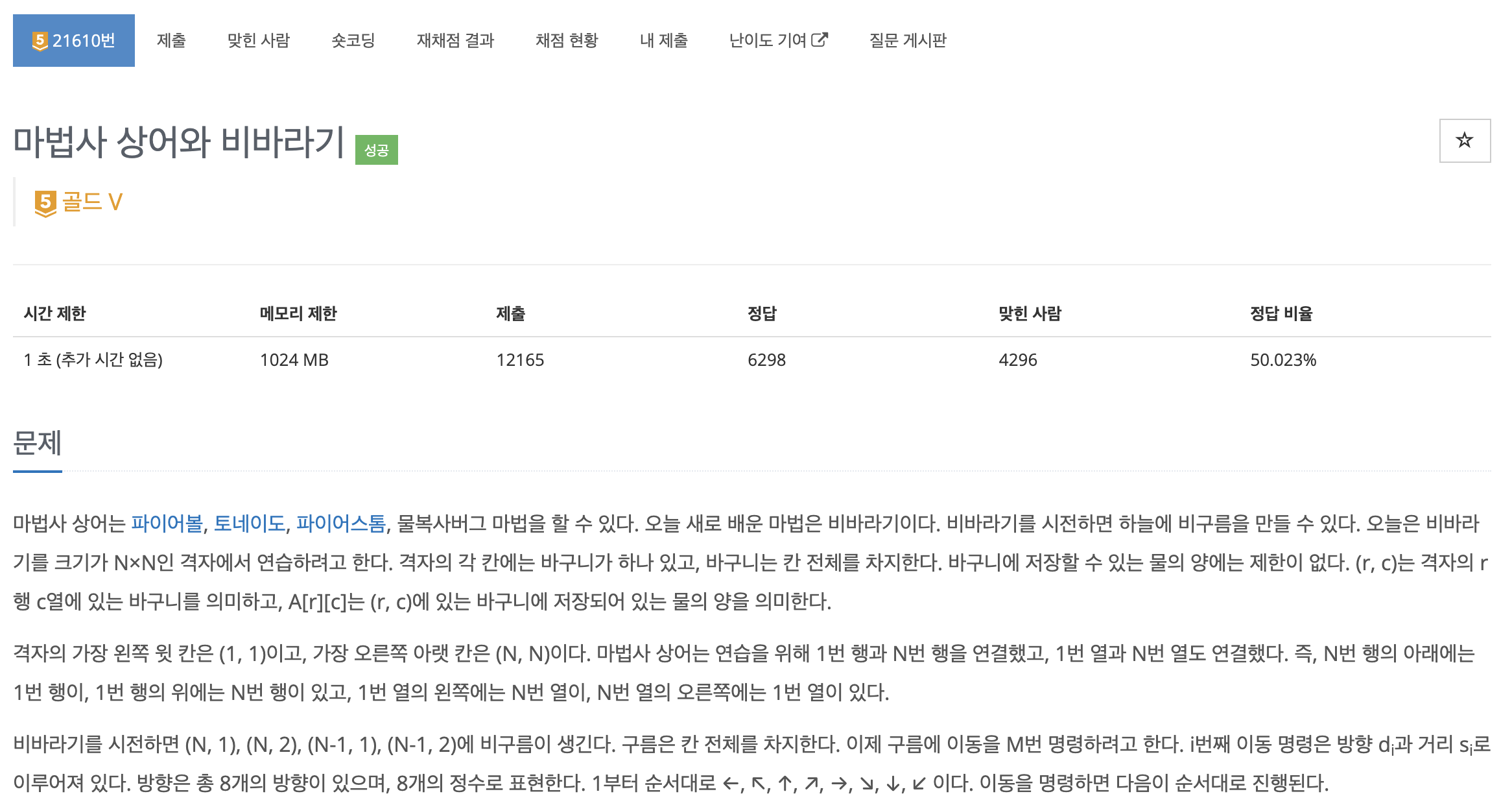
print(total)이번 문제는 전형적인 구현 문제로, 주어진 조건에 따라 2차원 배열인 구름의 좌표를 기준으로 이동시키고 값을 갱신해주는 방식의 문제이다.
처음에 문제를 보자마자 다음과 같이 기능을 나누어서 함수를 구현하였다.
- 구름을 이동시키고 물의 양을 1 증가시키는 함수(move)
- 물복사버그 마법을 사용하는 함수(waterCopy)
- 물의 양이 2 이상인 칸을 구름으로 생성하는 함수(createNewCloud)
오류 해결 1 (인덱스 에러)
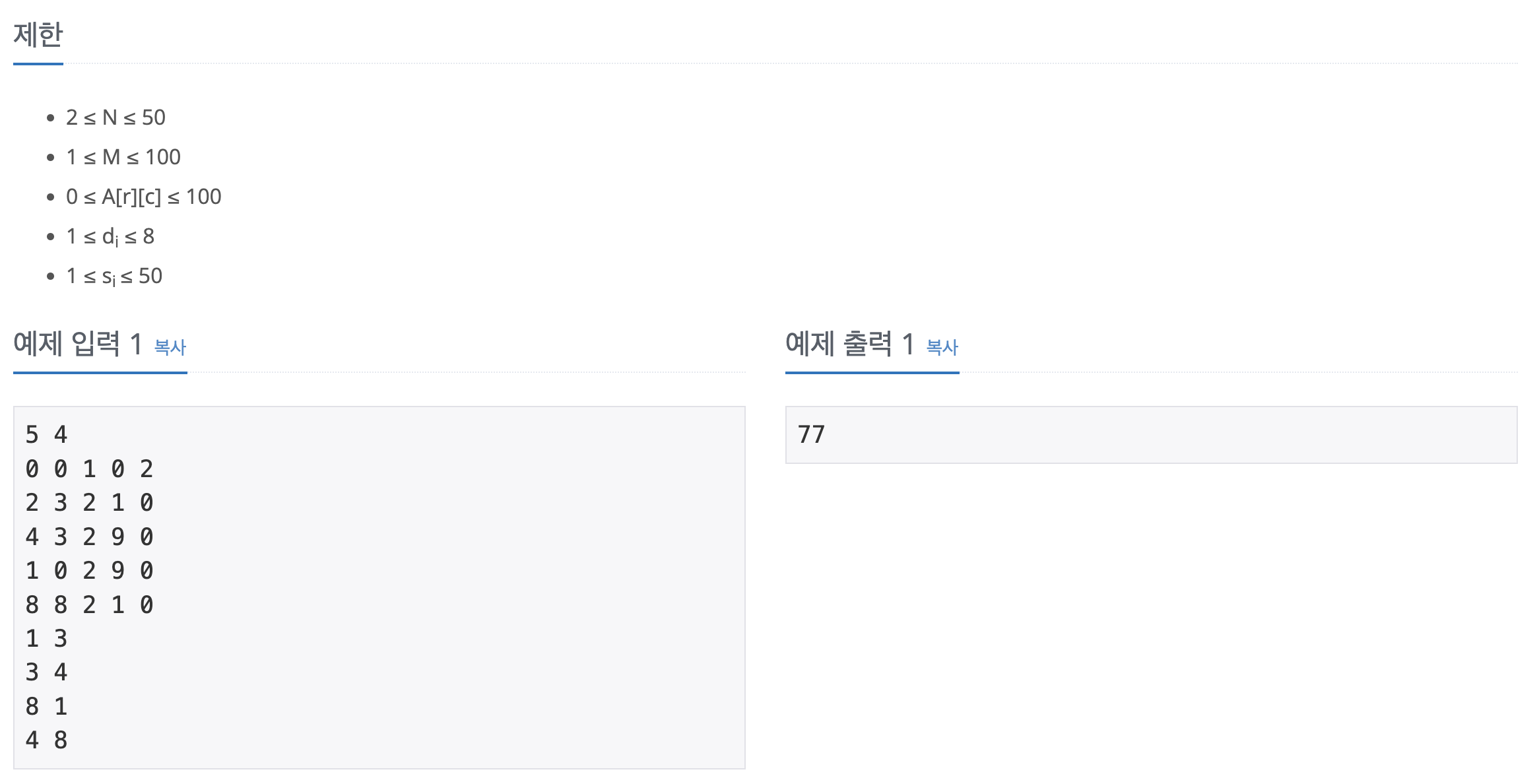
이 문제를 풀면서 첫번째로 마주하게 된 오류는 바로 리스트 인덱싱이었다. 양쪽의 행과 열이 연결되어 있다는 조건 때문에 2차원 배열의 인덱스의 범위를 넘어갔을 때 해당 범위 내의 인덱스로 변경시켜 주어야 했다.
temp_x = temp_x % n
temp_y = temp_y % n따라서 파이썬에서 배열의 인덱스가 범위를 넘어갈 때, 인덱스를 범위 내의 유효한 인덱스로 변경하기 위해 위와 같이 나머지 연산자(%)를 사용하는 방법으로 해결하였다.
오류 해결 2 (시간 초과)
두번째로 마주하게 된 오류는 시간초과이다. 처음에는 불필요한 반복문이나 연산때문에 발생한 것 인줄 알고 코드를 수정했지만 크게 개선이 되지 않아서 챗GPT에게 질문을 해본 결과 결정적인 문제는 "이때 구름이 생기는 칸은 3에서 구름이 사라진 칸이 아니어야 한다." 조건으로 인한 in 연산 때문이었다.
원래는 구름 목록(cloud_list)를 리스트 자료형(List)로 선언하고 새로운 구름이 기존 구름 목록에 존재하는지 확인하기 위해 in 연산을 하였는데, 리스트의 경우에는 특정 값이 존재하는지 유무를 찾기 위해서 최악의 경우 O(N)이 걸리게 된다.
하지만 이 문제에서는 좌표가 중복될 경우가 존재하지 않기 때문에, 집합 자료형(Set)을 사용하여 in 연산의 시간복잡도를 O(1)으로 최소화할 수 있다.
배운 점 및 느낀 점
- 시간초과가 발생했다면 불필요한 반복문이나 중복된 연산은 제거해보자.
- 중복된 값이 들어있지 않은 경우에는 리스트(List)가 아니라 집합(Set) 자료형을 사용하여 in 연산의 시간복잡도를 최소화하자.
'Algorithm 💡 > Implementation' 카테고리의 다른 글
| [백준 15686번] 치킨 배달 (0) | 2023.08.20 |
|---|---|
| [백준 14890번] 경사로 (0) | 2023.08.17 |
| [백준 14503번] 로봇 청소기 (0) | 2023.08.09 |
| [백준 15662번] 톱니바퀴(2) (0) | 2023.08.09 |
| [백준 14891번] 톱니바퀴 (0) | 2023.08.09 |



