
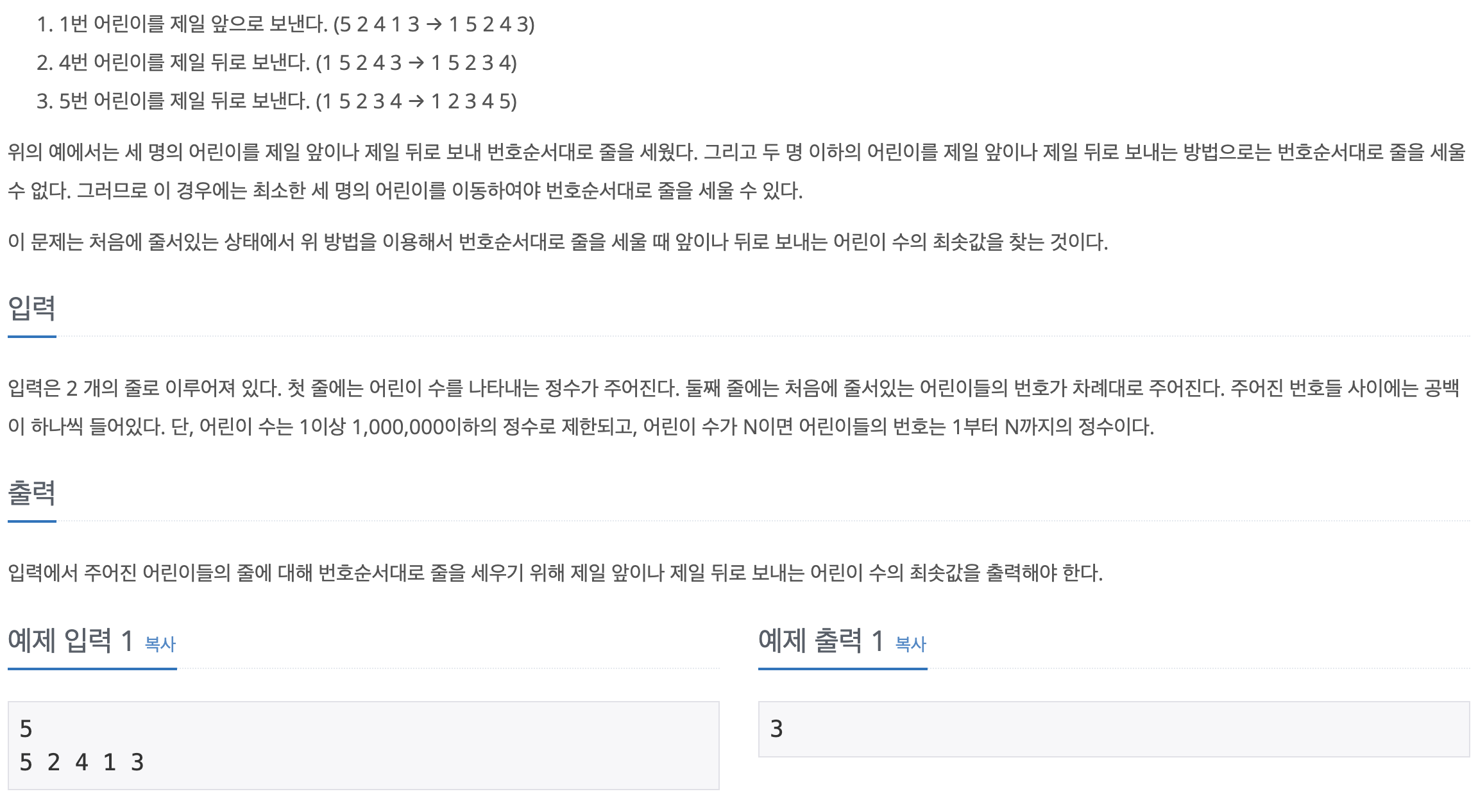

n = int(input())
data = list(map(int,input().split()))
data.insert(0,0)
index_list = [0]*(n+1)
count = 1
max_length = -1
for i in range(1,n+1):
index_list[data[i]] = i
for i in range(1,n):
if index_list[i] < index_list[i+1]:
count += 1
max_length = max(max_length, count)
else:
count = 1
if max_length != -1:
print(n - max_length)
else:
print(0)이번 문제는 임의의 순서로 세워진 번호를 맨 앞이나 맨 뒤로만 이동시킬 수 있다는 가정 하에 순서대로 배치하기 위한 최소한의 이동횟수를 구하는 문제이다.
이 문제는 바로 이전에 풀이한 2631번(https://woohyun-king.tistory.com/211) 문제와 유사한데, 2631번은 맨 앞과 맨 뒤를 포함한 어느 위치든 다 보낼 수 있지만 7570번 문제는 맨 앞이나 맨 뒤로만 보낼 수 있다는 차이점이 있다.
[백준 2631번] 줄세우기
n = int(input()) data = [] dp = [1]*n for i in range(n): data.append(int(input())) for i in range(n): for j in range(i): if data[i] > data[j]: dp[i] = max(dp[i],dp[j]+1) print(n - max(dp)) 이번 문제는 임의의 순서로 세워진 번호를 번호 순
woohyun-king.tistory.com
2631번과 같은 경우에는 증가수열에 포함하는 번호는 고정한 채 나머지 번호만 움직이면 되기 때문에, 나머지 번호의 갯수만큼 이동하면 되기 때문에 쉽게 풀 수 있다.
하지만 이번 문제는 가장 긴 증가수열에 포함하지 않는 나머지 번호들의 움직임이 자유롭지 않기 때문에 가장 긴 증가수열을 찾되 "연속된 수"를 가진 증가수열을 찾아야 문제를 해결할 수 있다.
또한, 이전 LIS 문제처럼 단순히 2중 반복문을 통해 찾는다면, n의 수가 1000000개 이기에 시간 초과가 발생하게 된다.
각 번호에 대한 인덱스를 통해 해결한다면 O(n^2) 은 피할 수 있게 된다. 결국 1을 더한 수의 위치가 본인보다 뒤에 있어야만 연속된 증가수열이라는 것을 이용하면 된다.
LIS 알고리즘에 대해서 복습해보면서, 여러 알고리즘을 열심히 공부해야겠다고 느껴진 하루였다 ,, 🥲
'Algorithm 💡 > DP' 카테고리의 다른 글
| [백준 11659번] 구간 합 구하기 4 (0) | 2023.10.01 |
|---|---|
| [백준 2579번] 계단 오르기 (1) | 2023.10.01 |
| [백준 2631번] 줄세우기 (0) | 2023.08.14 |
| [HackerRank] Knapsack (0) | 2023.05.20 |
| [HackerRank] The Maximum Subarray (0) | 2023.05.15 |



