
from copy import deepcopy
from collections import deque
import sys
sys.setrecursionlimit(10**7)
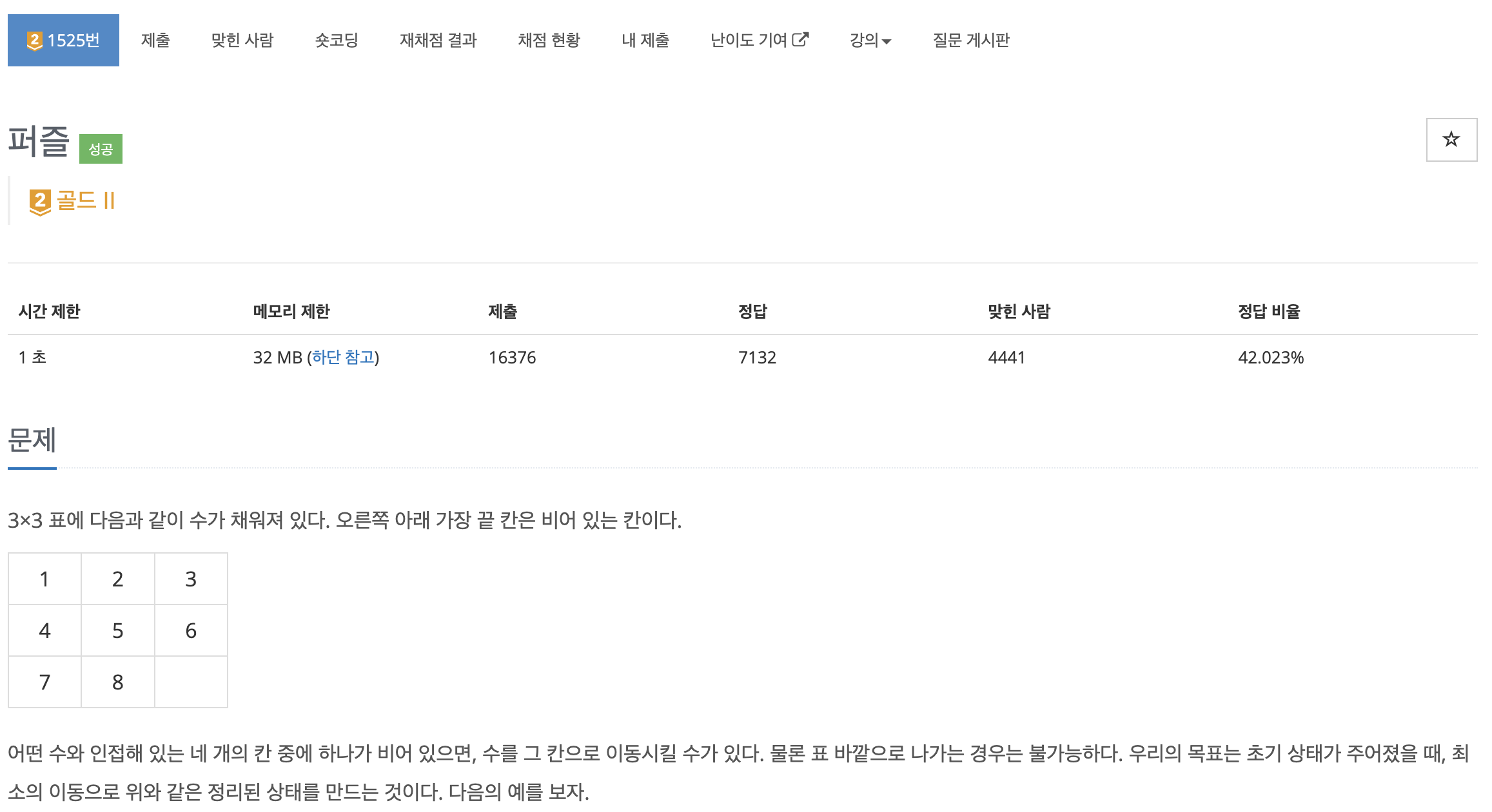
graph = [list(map(int,input().split())) for _ in range(3)]
final_graph = [[1,2,3],[4,5,6],[7,8,0]]
dx = [-1,1,0,0]
dy = [0,0,-1,1]
visited = {}
temp_graph = deepcopy(graph)
for i in range(3):
for j in range(3):
if graph[i][j] == 0:
first_x, first_y = i, j
def changeToString(arr): # 퍼즐의 상태를 문자열로 바꿔주는 함수
str_arr = []
for i in range(3):
for j in range(3):
str_arr.append(str(arr[i][j]))
return "".join(str_arr)
def bfs(): # BFS 함수
visited[changeToString(graph)] = 0
queue = deque([(first_x,first_y,graph,0)])
while queue:
v = queue.popleft()
x, y, g, c = v[0], v[1], v[2], v[3] # x값, y값, 그래프 상태, 이동거리
changed_g = changeToString(g) # 그래프 상태 문자열로 변환
if changed_g == '123456780': # 그래프 상태가 최종 상태랑 동일할 경우 Return
return visited[changed_g]
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if 0 <= nx < 3 and 0 <= ny < 3:
temp_g = deepcopy(g)
temp_g[x][y], temp_g[nx][ny] = temp_g[nx][ny], temp_g[x][y] # 값 변경
changed_temp_g = changeToString(temp_g)
if changed_temp_g not in visited: # 다음 좌표가 방문한 적이 없다면
visited[changed_temp_g] = c+1 # 사전 자료형에 저장
queue.append((nx,ny,temp_g,c+1)) # 큐에 삽입
return -1 # 큐에 더 이상 데이터가 없다면, 즉 최종 상태에 도달할 수 없다면 -1 반환
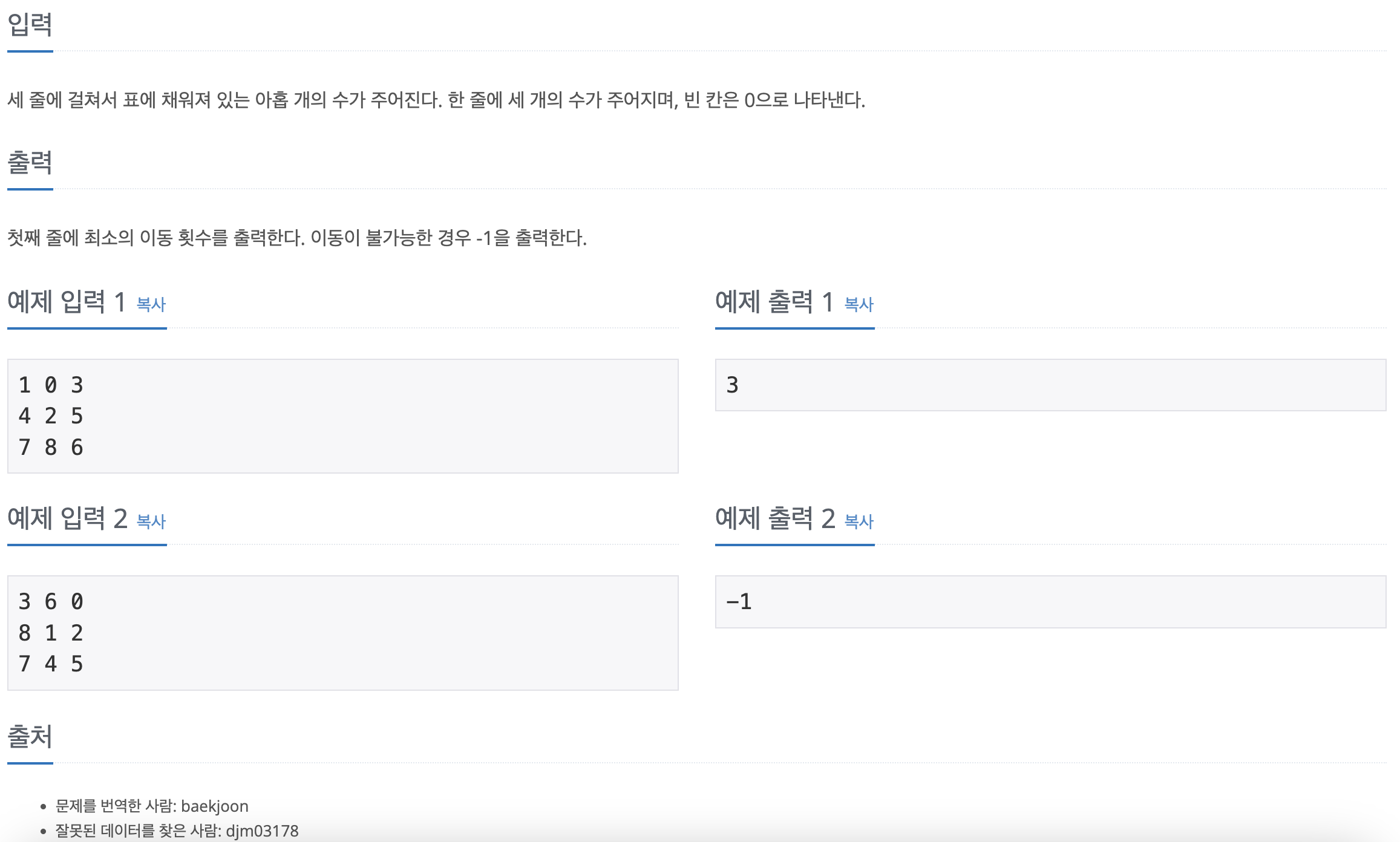
print(bfs())이번 문제는 주어진 퍼즐을 최소한의 이동으로 정리된 상태로 만드는 문제이다.
처음에는 이 문제를 DFS와 백트래킹을 사용해서 풀이하려고 했는데 DFS로 풀이하게 되면 정답이 정확하게 나오지 않게 되고, 또한 방문 여부를 현재 위치를 기준으로 확인하게 되면 최대 8번까지만 움직일 수 있게 되며 같은 위치를 다시 방문할 수 없게 된다.
하지만 이 문제는 최종 상태가 되기까지 같은 자리에 다시 방문해야 하는 경우가 있는 것으로 보인다.
그리고 BFS는 최초 방문한 점이 항상 최단 거리로 방문했음을 보장할 수 있기 때문에 방문 여부가 위치가 아니라 3X3 배열의 상태 자체를 저장해서 방문 여부를 확인해야 했고, 2차원 배열 값을 문자열로 변환(changeToString)하여 사전 자료형(visited)에 저장하였다.
ex) [[1,2,3], [4,5,6], [7,8,0]] 👉🏻 "123456780"
이렇게 현재 좌표의 상태를 딕셔너리의 key로 주고, 이동 횟수(c)를 value로 몇 번 만에 이 위치에 도착하였는지 저장해준 뒤 최종 상태("123456780")에 도달하였을 때 그 value는 최소 이동 횟수가 될 것이다.
이 문제를 풀고, 다른 사람들의 풀이를 통해 배운 점은 다음과 같다.
- DFS는 최단 및 최소 문제에 적합하지 않다.(현재 도달한 상태가 최단으로 도달했다는 보장이 없기 때문)
- 찾고자 하는 정답의 단계가 정해져 있거나 끝까지 도달해야 최적의 값을 찾는(모든 경우의 수를 따져보아야 하는) 문제라면 DFS가 유리하다. 즉, 경우의 수 세기나 재귀적 성질을 이용한 문제라면 DFS를 사용하자.
- 모든 경우의 수를 고려하는 것이 아니라 최단이나 최소 단계를 구하는 문제라면 BFS를 사용하자.
'Algorithm 💡 > BFS' 카테고리의 다른 글
| [SWEA 5102번] 노드의 거리 (1) | 2023.09.21 |
|---|---|
| [SWEA 5105번] 미로의 거리 (0) | 2023.09.21 |
| [백준 16234번] 인구 이동 (0) | 2023.08.07 |
| [백준 2206번] 벽 부수고 이동하기 (0) | 2023.08.04 |
| [백준 14923번] 미로 탈출 (0) | 2023.08.04 |



