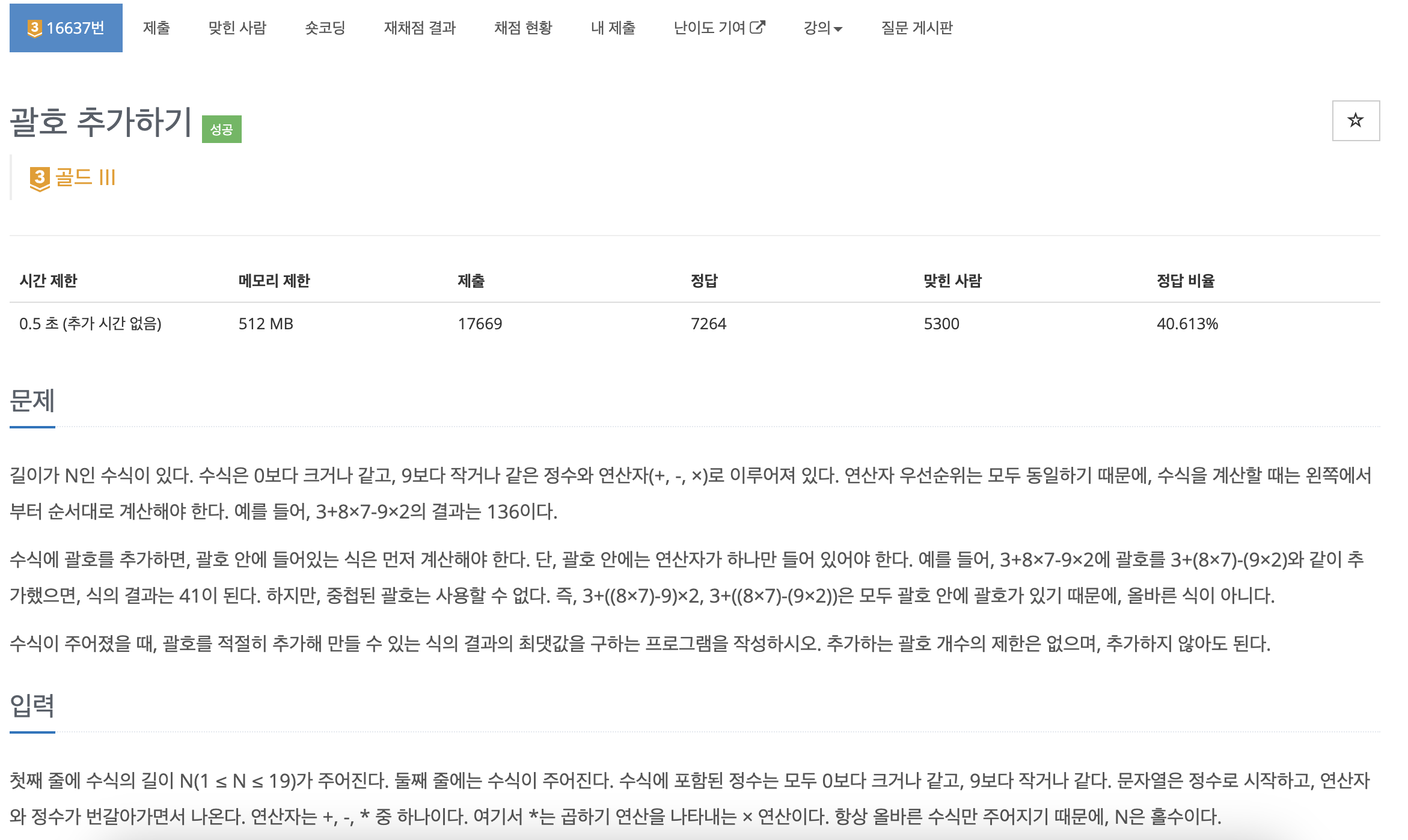
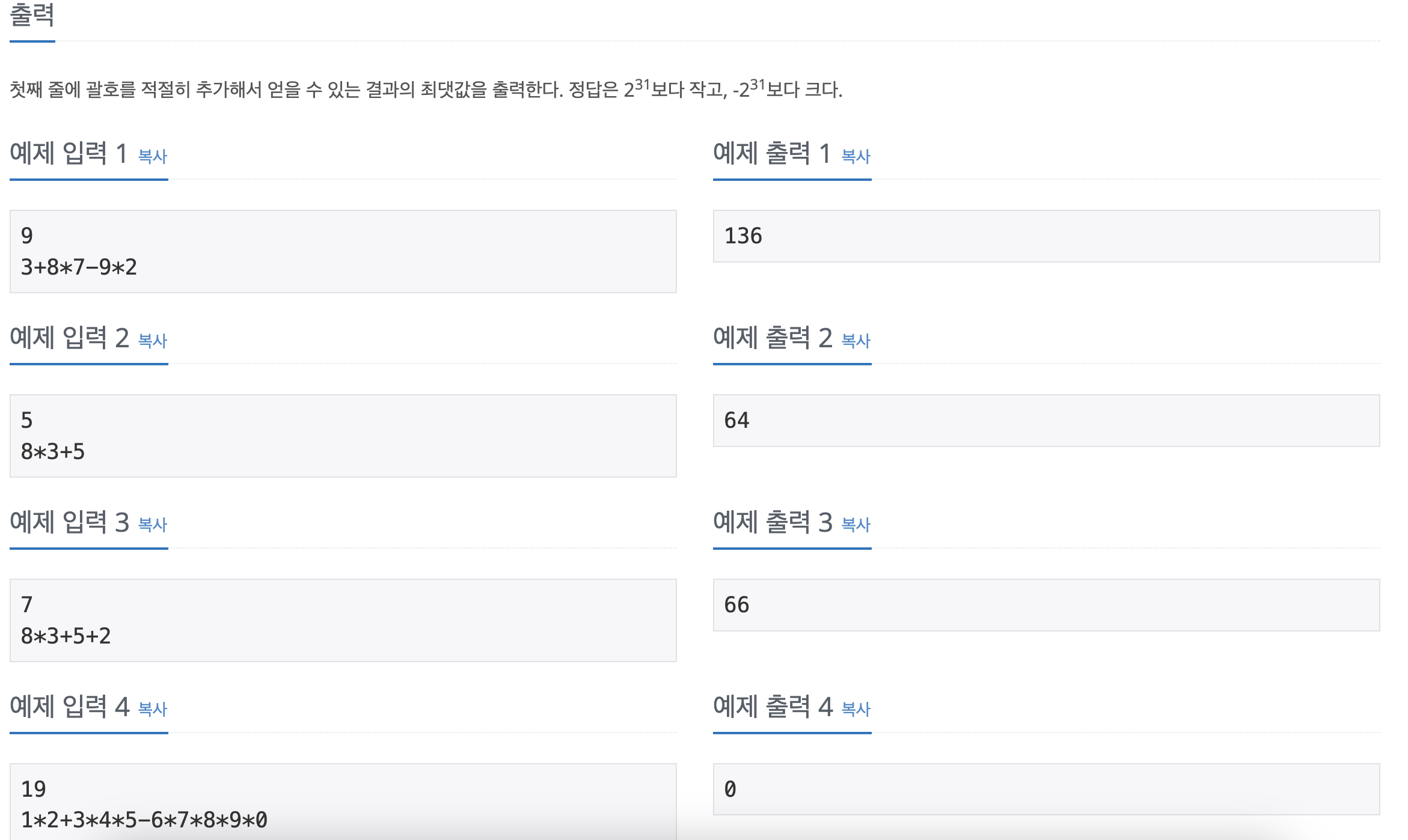
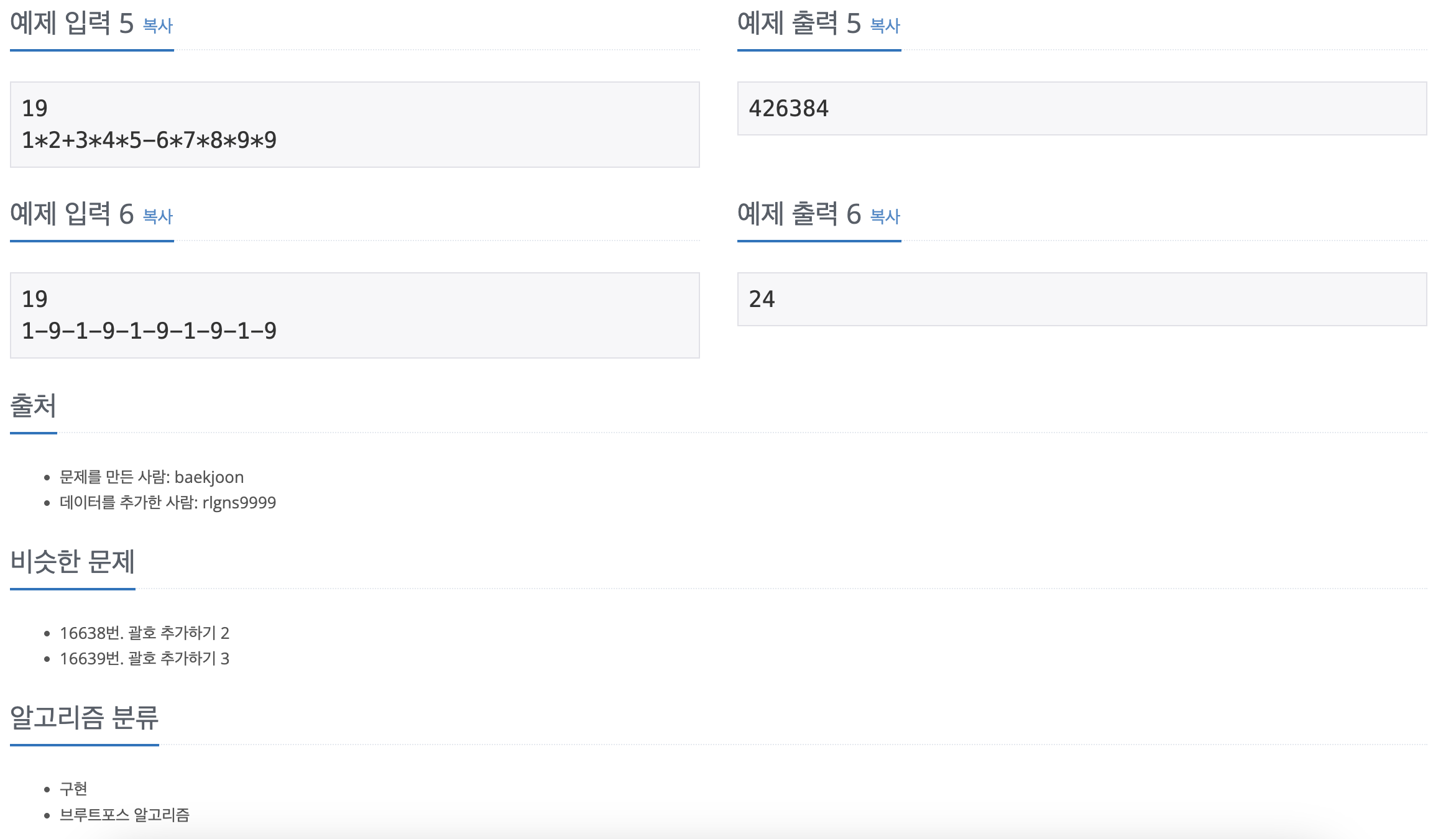
# 우선순위 X, 중첩괄호 X, 괄호 없어도 Ok
# 괄호 안에는 연산자 1개만 가능
# 괄호를 적절히 추가해서 최대값 만들기
n = int(input())
formula = list(input())
# 최대값 초기화
max_value = float("-inf")
# 주어진 값 2개를 연산하는 함수
def calculate(num1,operator,num2):
if operator == '+':
return num1 + num2
elif operator == '-':
return num1 - num2
elif operator == "*":
return num1 * num2
def dfs(index,value):
global max_value
# dfs로 마지막 값까지 계산을 마쳤을 경우
if index == n - 1:
max_value = max(max_value,value)
return
# 1. 괄호로 묶지 않고 바로 다음 숫자와 연산
if index + 2 < n:
dfs(index+2, calculate(value, formula[index+1], int(formula[index+2])))
# 2. 괄호로 묶고 다음 숫자와 다다음 숫자를 연산한 결과와의 연산
if index + 4 < n:
dfs(index+4, calculate(value, formula[index+1], calculate(int(formula[index+2]), formula[index+3], int(formula[index+4]))))
# 첫 번째 값부터 시작하여 dfs 알고리즘 실행
dfs(0,int(formula[0]))
print(max_value)이번 문제는 주어진 수식에 괄호를 적절하게 추가하여 최대값으로 만드는 문제이다.
처음에 이 문제를 접근했을 때는 수식의 맨 앞부터 값을 비교해가며 Greedy하게 풀이하려고 했었는데, 곰곰히 생각해보니 지금 당장 값이 크다고 해서 뒤에 있는 수식들을 계산했을 때 값이 무조건 크다는 보장이 없기 때문에 이 풀이방식은 잘못되었다는 것을 인지하였다.
하지만 풀이방법이 잘 떠오르지 않아 다른 사람의 풀이에서 힌트를 얻었는데, 바로 완전탐색(Brute-force) 알고리즘을 사용하는 것이다.
따라서 수식을 연산할 수 있는 모든 경우의 수를 따져보아야 했고, 각 위치에서 선택할 수 있는 경우의 수는 다음과 같다.
# 1. 괄호로 묶지 않고 현재 숫자와 바로 다음 숫자와 연산
if index + 2 < n:
dfs(index+2, calculate(value, formula[index+1], int(formula[index+2])))
# 2. 다음 숫자와 다다음 숫자를 괄호로 묶고 연산한 결과를 현재 숫자와 연산
if index + 4 < n:
dfs(index+4, calculate(value, formula[index+1], calculate(int(formula[index+2]), formula[index+3], int(formula[index+4]))))- 괄호로 묶지 않고 현재 숫자(value)와 바로 다음 숫자(int(formula[index+2]))와 연산
- 다음 숫자와 다다음 숫자를 괄호로 묶고 연산한 결과(calculate(int(formula[index+2]), formula[index+3], int(formula[index+4])))를 현재 숫자(value)와 연산
# dfs로 마지막 값까지 계산을 마쳤을 경우
if index == n - 1:
max_value = max(max_value,value)
return위와 같은 로직으로 마지막 인덱스에 도착했을 때, 즉 마지막 값까지 연산을 마쳤을 때 모든 경우의 수를 max_value와 비교하여 최대 값을 업데이트 해주는 방식으로 풀 수 있었다.
이번 문제는 완전탐색 알고리즘 중 DFS를 사용하여 모든 경우의 수를 탐색해가며 최종적으로 최대값을 찾는 문제였는데, 항상 2차원 배열을 활용한 DFS/BFS에만 적응되어 있다보니 이러한 문제에서 자주 막히는 것 같다. Brute-force 문제를 자주 풀어봐야겠다고 느낀 문제였다 🥲
'Algorithm 💡 > DFS' 카테고리의 다른 글
| [백준 15684번] 사다리 조작 (0) | 2023.08.21 |
|---|---|
| [백준 16724번] 피리 부는 사나이 (0) | 2023.08.20 |
| [프로그래머스 Lv.3] 네트워크 (0) | 2023.07.31 |
| [프로그래머스 Lv.3] 여행경로 (0) | 2023.07.30 |
| [HackerRank] Count Luck (0) | 2023.05.19 |



