

def getWays(n, c):
# Write your code here
coin_count = len(c)
dp = [[0]*(n+1) for _ in range(coin_count+1)]
for i in range(1,coin_count+1):
dp[i][0] = 1
for i in range(1,coin_count+1):
for j in range(1,n+1):
coin_value = c[i-1]
if coin_value > j :
dp[i][j] = dp[i-1][j]
else:
dp[i][j] = dp[i-1][j] + dp[i][j-coin_value]
return dp[coin_count][n]이번 문제는 주어진 c 배열 안의 값들로 n을 만들 수 있는 경우의 수를 구하는 문제이다.
문제의 힌트에 적혀있는 것처럼 단순하게 완전 탐색(Burte-Force)을 사용하여 풀 경우, 각 원소를 사용하는 경우와 사용하지 않는 경우를 모든 원소에 관하여 경우의 수를 구해야 하므로 O(2^n) 시간이 걸리게 되어 시간초과가 발생할 것이다.
따라서 1번째 원소만 사용할 경우부터 1~2번째 원소만 사용할 경우 ... 1~n번째 원소를 사용할 경우를 DP 알고리즘을 사용하여 풀이해야한다.
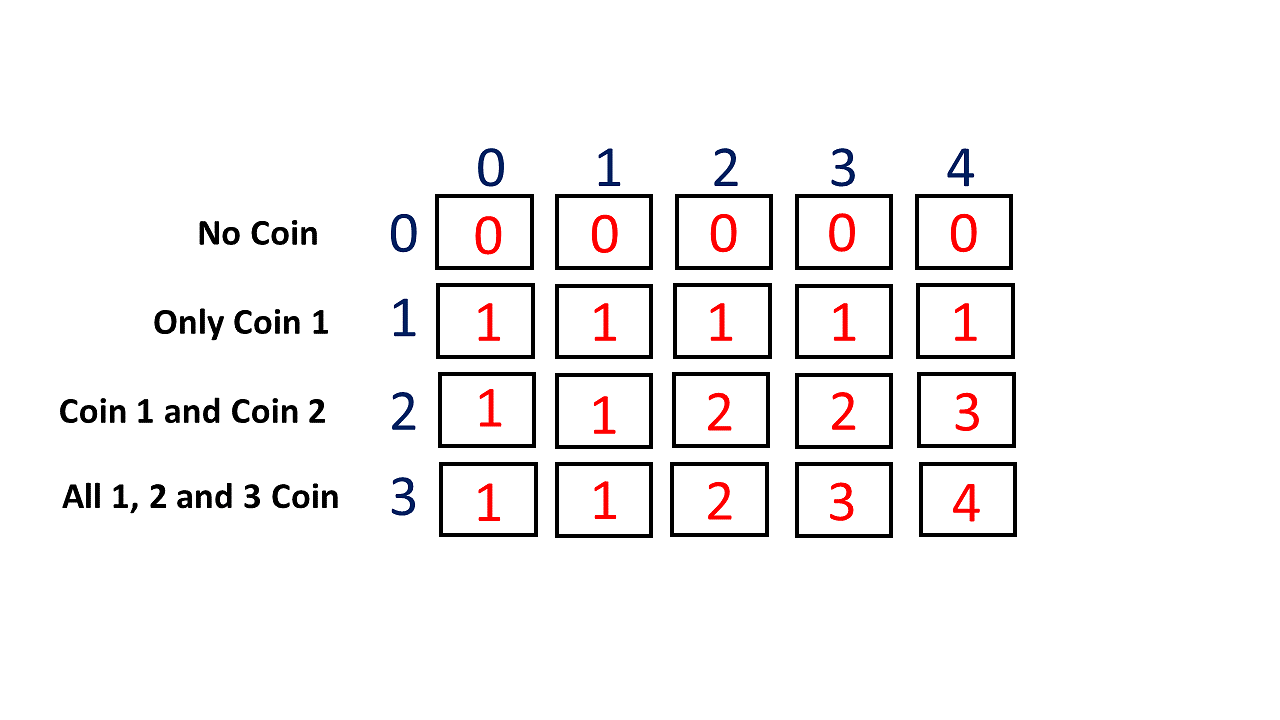
0-1 배낭 문제와 비슷하게 각 동전의 사용여부를 행으로, 만들고자 하는 값을 열로 설정하여 (동전 개수 + 1) * (타겟 값 + 1) 크기로 DP 테이블을 만들어서 풀이할 수 있었다.
점화식을 찾는데 시간이 걸리긴 했지만 이번 문제를 풀면서 DP 문제는 최대한 간단한 예시를 사용하여 DP 테이블을 채우거나, 직접 값을 구해보면서 점화식을 도출해내는 것이 가장 중요하다는 것을 깨달았다.
또한 2차원 DP 테이블을 생성할 경우 (고려해야 하는 값의 개수 + 1), (타겟 값 + 1) 의 크기로 2차원 리스트를 만들어서 각 1행과 1열에 들어갈 초기 값을 정확하게 설정해야 한다는 점을 배울 수 있었다 :)
'Algorithm 💡 > DP' 카테고리의 다른 글
| [HackerRank] Knapsack (0) | 2023.05.20 |
|---|---|
| [HackerRank] The Maximum Subarray (0) | 2023.05.15 |
| [백준 16194번] 카드 구매하기 2 (0) | 2023.05.04 |
| [백준 2293번] 동전1 (0) | 2023.04.11 |
| [백준 1520번] 내리막 길 (0) | 2023.04.10 |



