n = int(input())
soluton = 0
# 먼저 3의 배수인 경우랑 5의 배수인 경우 처리
# 3의 배수는 3의 개수를 5로 나눠서 몫 *3 + 나머지
if n%3 == 0:
soluton = n // 3
soluton = ((soluton//5)*3) + (soluton%5)
# 5의 배수는 그대로
elif n%5 == 0:
soluton = n//5
# 5를 먼저 빼고 3으로 나눠지는지 확인
# 3으로 나눠지면 3으로 나눠서 그 몫을 더해주고 끝
# 3으로 나눠지지 않으면 5 한번더 빼기
else:
while n != 0:
# n이 1~2 이 되면 답이 X
if n < 3 and n > 0:
soluton = -1
break
# 5보다 크거나 같은 경우엔 5빼기
if n >= 5 :
soluton += 1
n -= 5
# 3,4인 경우
elif n>=3:
soluton += 1
n -= 3
if n%3 == 0:
# soluton += n//3
temp = n//3
soluton += ((temp//5)*3) + (temp%5)
n %= 3
print(soluton)이번 문제는 문제 티어와 내용에 비해서 정답률이 높지 않아 의아했었는데, 직접 풀어보니 그 이유를 알 수 있었다.
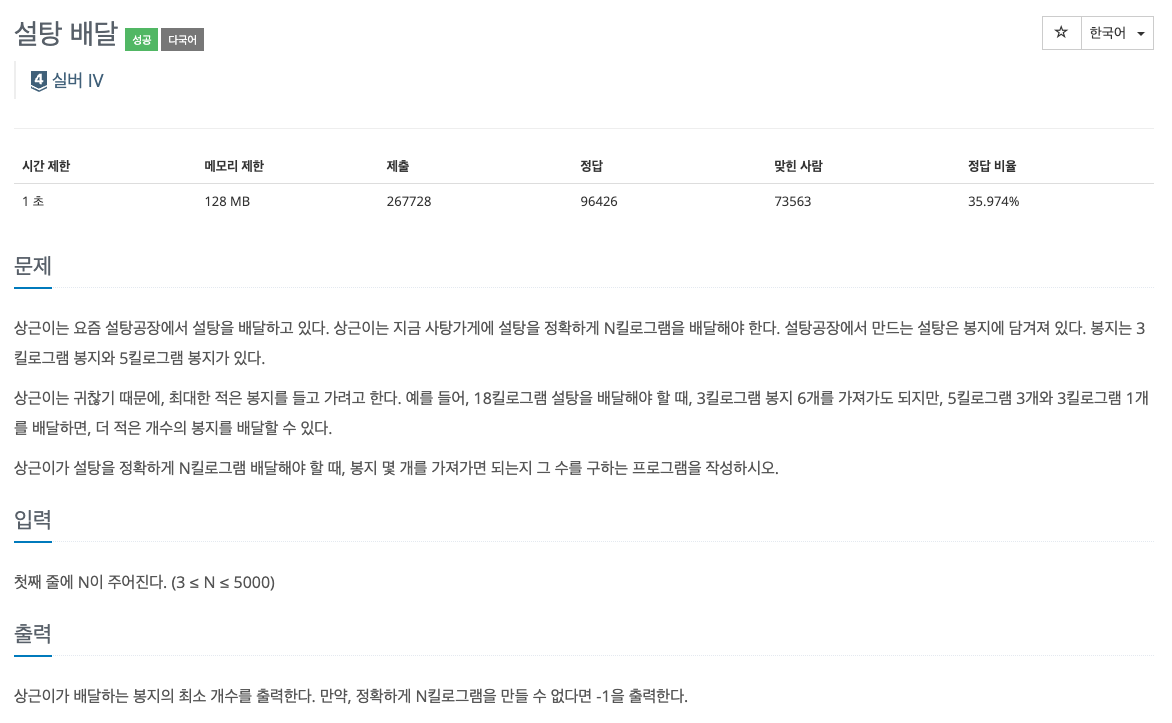
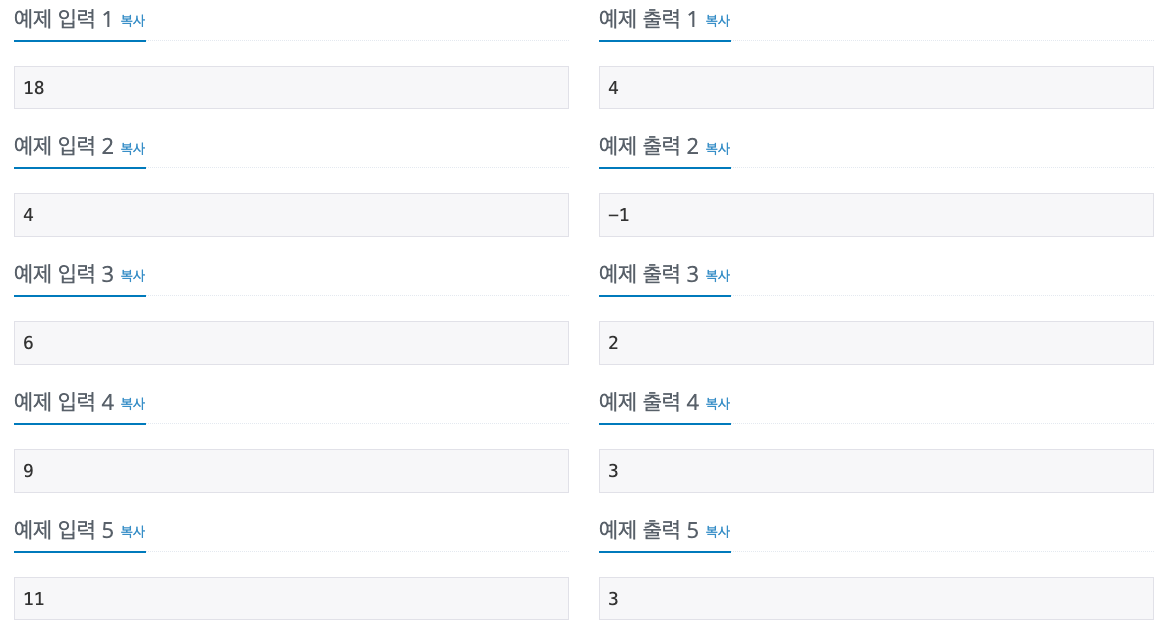
이 문제의 핵심은 5와 3으로 만들 수 있는 수를 "5를 최대한 많이" 사용하여 정답을 구하는 것이다.
첫번째 접근은 3과 5의 배수를 먼저 처리해주는 것 이었는데, 3의 배수인 경우에는 15(3과 5의 최소 공배수)가 넘어가는 경우에는 15(3*5)를 15(5*3)으로 변경하여 최대한 봉지의 개수를 줄여주었다.
두번째 접근은 3과 5의 배수가 아닌 수인데, 이 경우에는 n이 3과 5의 조합으로 만들 수 있는지 없는지를 먼저 따져봐야 한다.
따라서 n을 계속 업데이트 시켜주되, n이 0이 되는 경우(3과 5의 조합으로 만들 수 있는 경우)에는 while문을 빠져나오도록 하고 n이 3보다 작은 경우(3과 5의 조합으로 만들 수 없는 경우)에는 -1을 반환하도록 하였다.
마지막으로 위에서 언급했던 n을 업데이트 시켜주는 작업인데, 첫번째 접근에서 이미 5의 배수와 3의 배수를 처리했기 때문에 이제 남은 것은 최대한 5를 많이 사용하는 것이다.
그래서 먼저 n에서 5를 뺄 수 있으면 빼주고, 만약에 3으로만 뺄 수 있다면 3을 빼준 뒤에 ..
그 결과가 3으로 나눠지는 경우라면 바로 3을 나눈 몫을 봉지의 개수에 더해주는데, 여기서 중요한 것은 여기에서도 3이 5개 이상인 경우가 있다는 것이다. (이 케이스 때문에 한번 틀렸다고 한다 🥲)
이렇게 3가지 접근을 통해 끝내 맞힐 수 있었는데, Greedy 알고리즘을 푸는 경우에도 무작정 탐욕적으로 푸는 것이 아니라 예외를 항상 생각해야 한다는 것을 느낄 수 있던 문제였다.
'Algorithm 💡 > Greedy' 카테고리의 다른 글
| [백준 11047번] 동전 0 (0) | 2023.02.07 |
|---|---|
| [백준 11399번] ATM (0) | 2023.02.06 |
| [이코테] 무지의 먹방 라이브 (0) | 2023.02.05 |
| [이코테] 볼링공 고르기 (0) | 2023.02.02 |
| [이코테] 만들 수 없는 금액 (0) | 2023.02.02 |



