n = int(input())
data = []
dp = [1]*n
for _ in range(n):
data.append(list(map(int,input().split())))
data.sort(key=lambda x:x[0])
for i in range(1,n):
for j in range(i):
if data[i][1] > data[j][1]:
dp[i] = max(dp[i], dp[j]+1)
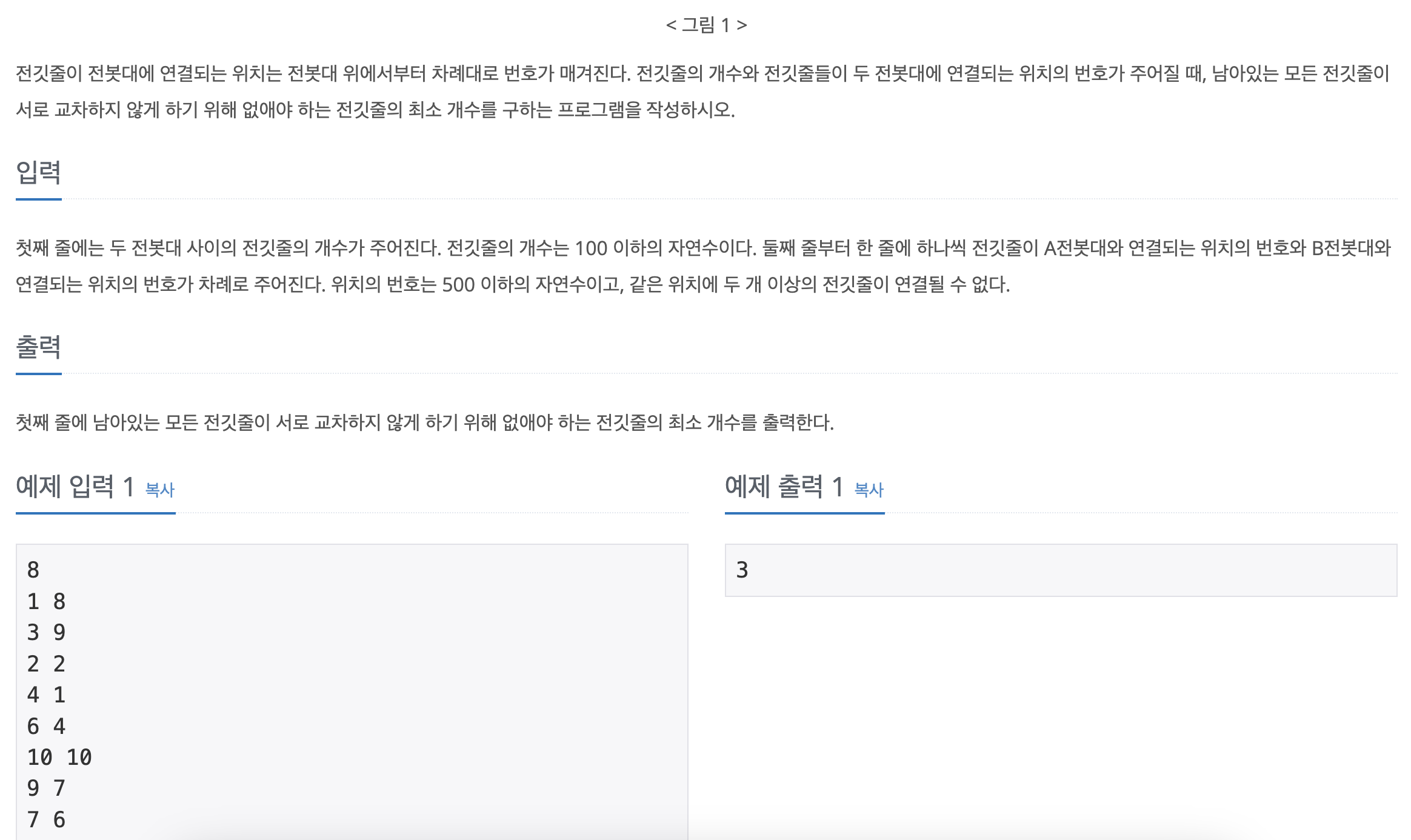
print(n-max(dp))이번 문제는 A와 B 전봇대 사이에 연결된 전깃줄의 정보와 전깃줄의 개수가 주어졌을 때, 모든 전깃줄이 서로 교차하지 않도록 하기 위해 제거해야 하는 전깃줄의 최소 개수를 구하는 문제이다.
처음에 이 문제를 접했을 때 이전에 풀던 DP 방식(n=1 부터 구하면서 점화식을 찾는 방식)으로 풀려고 해보았지만 당연히 이 방식으로 풀 수 있는 문제가 아니었고, 교차하는 전깃줄의 개수를 구해보려고 했지만 생각보다 복잡할 것 같아 이 방법도 아니라는 것을 깨달았다.
다른 분의 풀이를 참고한 결과, 이 문제의 핵심은 제거해야 하는 전깃줄의 개수를 세는 것이 아니라 '교차하지 않는 조건을 고려하여 오름차순인 가장 긴 부분수열(LIS)을 구하는 것'이었다.
따라서 A 전봇대를 기준으로 오름차순으로 정렬한 뒤, B 전봇대를 기준으로 LIS를 구하고 나서 문제의 정답은 교차하지 않도록 만들기 위해 제거해야 하는 전깃줄의 개수이므로 전체 전깃줄 개수(n)에서 LIS 값(max(dp))을 빼줌으로써 정답을 구할 수 있었다.
https://woohyun-king.tistory.com/115
[백준 18353번] 병사 배치하기
import sys input = sys.stdin.readline n = int(input()) data = list(map(int,input().split())) dp = [1]*n for i in range(1,n): for j in range(i): if data[i] < data[j]: dp[i] = max(dp[i],dp[j]+1) print(n - max(dp)) 이번 문제는 병사의 수 N과 각 병
woohyun-king.tistory.com
이 문제는 '18353번 : 병사 배치하기' 문제와 상당히 유사한데, Bottom-Up 방식으로 점화식을 구하는 것이 아니라 LIS를 활용하여 풀이하는 유형으로 보인다.
위 문제와 공통점은 문제에서 '열외시켜야 할 병사의 수', '제거해야 하는 전깃줄의 개수' 처럼 기존 값에서 제거하는 방식으로 풀이하도록 유도하여 헷갈리게 한다는 점이다.
교차하지 않는 조건(A 기준으로 오름차순으로 정렬했을 때, B에서 오름차순을 이룬다는 것은 교차하지 않는다는 것)을 생각해냈다면 풀 수 있었을텐데 조금 아쉽다는 생각이 들었다.
앞으로는 문제를 풀이할 때 직관적으로 풀이하려는 습관을 버려야겠다는 생각이 들었던 문제였다 :)
'Algorithm 💡 > DP' 카테고리의 다른 글
| [백준 1520번] 내리막 길 (0) | 2023.04.10 |
|---|---|
| [이코테] 금광 (0) | 2023.03.27 |
| [백준 9251번] LCS (0) | 2023.03.23 |
| [백준 14501번] 퇴사 (0) | 2023.03.22 |
| [백준 2193번] 이친수 (0) | 2023.03.22 |



